Gdzie jest błąd w rozumowaniu.
Bedekopacrowy: Gdzie jest błąd w rozumowaniu?
|x+2| + |3−x| ≤ 5
Opiszę w krokach:
Najpierw wyznaczam 3 przedziały(na podstawie definicji modułu):
1) (−∞,−2)
2) <−2,3>
3) (3,+∞)
i rozwiązuje tą nierówność dla tych 3 przedziałów z odpowiednimi znakami np. w 1 przypadku
znaki modułów to − i + dla kolejnych.
Następnie wyniki porównuje z dziedziną przypadku czyli (−∞,−2) itd.
I tu jest problem jak porównuje z dziedziną przypadków to mam zły wynik a jak nie porównuje to
mam dobry gdzie robie błąd?
6 lis 23:12
Adamm: |x+2|+|3−x|≥|3−x+x+2|=5
|x+2|+|3−x|=5
6 lis 23:15
Bedekopacrowy: Co?!
6 lis 23:19
Adamm: |x|+|y|≥|x+y|
musi zachodzić równość
6 lis 23:22
Bedekopacrowy: No dobra fajnie, ale ja nie korzystam z tego wzoru w moim rozwiązaniu. Proszę o wskazanie błędu
w rozumowaniu a nie kolejnego pomysłu do rozwiązania zadania.
6 lis 23:27
Mila:
|a|+|b|≥|a+b|
Czyli najmniejszą wartością
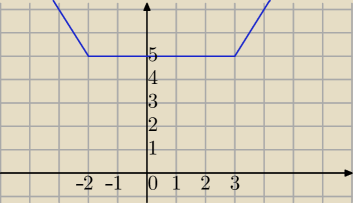
f(x)=|x+2|+|3−x| jest liczba 5
Warunek
|x+2|+|3−x|≤5 jest spełniony tylko w przypadku:
|x+2|+|3−x|=5 dla x∊<−2,3>
6 lis 23:29
jc: |a−b| = odległość pomiędzy a i b.
Suma odległości x od −2 i od 3 wynosi 5, czyli dokładnie tyle, ile odległość
pomiędzy −2 a 3. Oznacza to, że x ∊[−2,3].
6 lis 23:30
Bedekopacrowy: Całkowicie rozumiem rozwiązanie Mili, OK. Ale wciąż nie wiem gdzie leży błąd w moim
rozumowaniu.
6 lis 23:33
Adamm: błąd prawdopodobnie rachunkowy
6 lis 23:34
Bedekopacrowy: Otóż mam dobre rozwiązania dla natomiast przy porównaniu tego rozwiązania z dziedziną przypadku
otrzymuje zbiór pusty.
6 lis 23:37
Bedekopacrowy: Otóż mam dobre rozwiązania dla każdego przypadku natomiast przy porównaniu tego rozwiązania z
dziedziną przypadku
otrzymuje zbiór pusty.
6 lis 23:38
jc: Bedekopacrowy, o ile to możliwe, dobrze jest widzieć wynik, a nie liczyć.
W rachunkach można się pomylić.
6 lis 23:38
jc:
−2 ≤ x ≤ 3
|x+2| = x+2
|3−x | = 3−x
|x+2| + |3−x | = (x+2) + (3−x)=5
6 lis 23:40
Bedekopacrowy: Wtedy 5≤5 i dziedzina przypadku to −2≤ x ≤ 3 czyli mamy ∅
6 lis 23:42
Bedekopacrowy: Aha nie jestem debilem
6 lis 23:43
Bedekopacrowy: Ide kopac rowy
6 lis 23:43
Mila:
Jutro napiszę w przedziałach

Dobranoc.
6 lis 23:47
Bedekopacrowy: Nie Mila nie pisz, już jest ogarnięte dzięki i dobranoc. Po prostu dla mnie <−2,3> ∩ R=∅, i nie
widze tego przez godzine

6 lis 23:50
Mila:

6 lis 23:51
 |a|+|b|≥|a+b|
Czyli najmniejszą wartością
f(x)=|x+2|+|3−x| jest liczba 5
Warunek
|x+2|+|3−x|≤5 jest spełniony tylko w przypadku:
|x+2|+|3−x|=5 dla x∊<−2,3>
|a|+|b|≥|a+b|
Czyli najmniejszą wartością
f(x)=|x+2|+|3−x| jest liczba 5
Warunek
|x+2|+|3−x|≤5 jest spełniony tylko w przypadku:
|x+2|+|3−x|=5 dla x∊<−2,3>
 Dobranoc.
Dobranoc.

