dziedzina Edi: Jaka będzie dziedzina funkcji: f(x) = 4 ^x−1_x+5 , dla x≥1

kalafiorowa: x∊<1;5)∪(5;+niesk.)

Edi: dlaczego do 5?

Edi: mi sie wydawalo ze od 1 do nieskonczonosci

mela: D_f = <1,∞) bo x ≠ −5 i x ≥ 1 => x€ <1,∞)

Edi: a czy moglby ktos dalsza procedure badania funkcji zrobic..? policzylem limes +∞ i 1 , tylko nie wiem czy jednyka bedzie lewo czy prawostronna... i czy tylko tych dwoch licze wyszlo mi ze lim +∞ = 4, a lim 1 = 0 czyli wynika z tego ze 4 jest asymptota pozioma? a 0 pionowa...? w ukośnej wychodzi mi ze bedzie to y=4 wiec chyba cos nie tak... przy ekstremum ze −5 jest podejrzane o nie i monotonicznosc od −∞ do −5 rosnie, a od −5 do +∞ maleje z punktami przegiecia juz nie wiem jak jest. policzylem druga pochodna i nie wiem co dalej.. moglby ktos cos podpowiedziec co do tego przykłądu bo wydaje mi się ze nie jest to dobrze...

Edi:

Mickej: kalafiorowa podała złą dziedzine z dziedziny wykreślasz tylko −5

ula: y=4 to asymptota pozioma obustronna 0 należy do dziedziny więc należy do wykresu

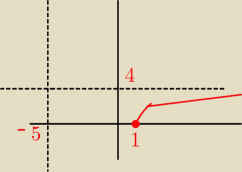
ula: wyjdzie tak jak na rysunku

Bogdan: Dobry wieczór.

	x − 1
f(x) = 4
	x − 5

Dziwnie zapisana funkcja, czy na pewno taki jest jej wzór?

ula: jest to zwykła funkcja homograficzna dla x≥1

	−24
y=		+4
	x+5

Bogdan: Edi wypowiedz się w sprawie wzoru tej funkcji