Monotonicznosc funkcji 5-latek: Zbadaj monotonicznosc ponizszych funkcji (okresl najpierw dziedzine funkcji Przyklady oprocz nr 1 (a mam 10 funkcji sa ciezkie wedlug mnie No ale postarm sie sprobowac Nr 1 f(x)= x² d_f= R Znam wykres tej funkcji i wiem ze ona nie jest monotoniczna w calym zakresie

	1
Nie jest ani rosnaca bo np (−1)<		to f(−1)>f(0,5)
	2

Nie jest takze malejaca bo np (−1)<2 to f(−1)<f(2) Ale jest monotoniczna przedzialami Teraz nr 2

	1
f(x)=
	1+x2

D_f= R Tez wiem jak wyglada wykres tej funkcji . Tez jest ona przedzialami monotoniczna Jak tutaj wykazac monotonicznosc ?

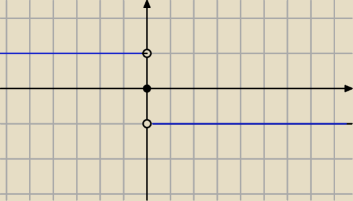
5-latek: A ta tak samo poradzielem sobie jak z 1 Teraz nr 3 f(x)= 1 dla x<0 0 dla x=0 −1 dla x>0 jak tutaj ?

5-latek:

5-latek:

5-latek: Moz eby jednak ktos pomogl tutaj mam x₁<x₂ ⇒f(x₁)>f(x₂) Autor jednak piszse ze f(x₁)≥f(x₂) Z rysunku widac zew przedzialach (−∞,0) (0∞) to funkcje stale ale np f(−3)= 1 f(5)=−1 to dlaczego piszse ≥?

5-latek: nr 4 f(x)= 1 dla x∊W 0 dla x∊NW Dlaczego ta funkcja nie jest monotoniczna ? Jak w ogole bedzie wygladal jej wykres ?

5-latek:

5-latek:

Janek191: Wykresu nie da się narysować. Pomiędzy dowolnymi dwoma liczbami wymiernymi znajduje się co najmniej jedna liczba niewymierna i odwrotnie, więc trudno tu mówić o monotoniczności.

5-latek: Inaczej to zrobie wobec tego nr 5 f(x)=( x² x∊Q (−x² x∊R\Q nr6) f(x)= (−x³ x≤0 (−x x>0 nr7 f(x)= (−e^x x≤0 (−x−1 x>0 Ta bedzie scisle malejaca Nr 8) f(x)= ( 0 x≤0 ( 3 0<x≤2 (4 x>2 nr 9 f(x)= √cos²x−1

5-latek: Witaj i pozdrawiam A z ta nr 3 ?

Jerzy: Cześć Zad 3) Rozpatruj w przedziałach

Janek191: nr 3 D = ℛ Jest to funkcja nierosnąca.

5-latek: Wiec przedzialami sa to funkcje stale wiec niemalejace czyli mozemy zapisac ze dla dowolnych x₁ x₂ z dziedziny f(x₁)= f(x₂) wiec takze f(x₁)≥f(x₂)

Jerzy: A dlaczego nie: "niemalejąca" ?

5-latek: Witaj A nie napisalem tak

Jerzy: Dla dowonych x₁,x₂ należących do D i takich,że x₁ > x₂ mamy f(x₁) ≤ f(x₂), czyli funkcja nierosnąca

Jerzy: Mój bład ... to funkcja nierosnąca ( czyli malejąca lub stała )

5-latek: Jerzy W tym repetytorium ma napisane ze funkcja stala jest szczegolnym przypadkiem funkcji rosnacej Wiec moze bede sie trzymal tego Ty oczywiscie masz racje ze moze ona byc takze nierosnaca

Jerzy: Ale to przypadek, gdy funkcja ma stałą wartość w całej dziedzinie, a tutaj od pewnego x jej wartośc zmalała.

5-latek: Dobrze ze to wlasnie napisales i teraz sie ja sie dobrze przypatrzylem i masz racje jest x₁<x₂ ⇒f(x₁)≥f(x₂) Zostawie to (sa za trudne dla mnie Znajde moze jakies inne takie zeby byly niesklejane