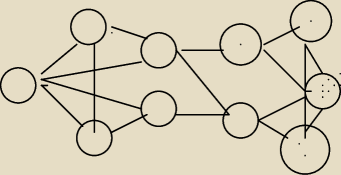
Ekscentryczność grafu Pomocy: Hej, czy jest ktoś w stanie mi wytłumaczyć w jaki sposób to się wyznacza? Znalazłam wiele definicji, ale one mi za wiele nie objaśniają. Rysunek nie jest super, ale taki poglądowy Wierzchołki są etykietowane i poniżej podam ich wartości w takiej kolejności jak one są 1 7 3 5 0 9 4 6 2 8 I mam podane ekscentryczności do każdego wierzchołka ex(0)=3 ex(1)=3 ex(2)=3 ex(3)=2 ex(4)=2 ex(5)=3 ex(6)=2 ex(7)=7 ex(8)=3 ex(9)=3 Może mi ktoś wyjaśnić skąd to wszystko się bierze? Samej definicji nie rozumiem, a przykład niestety nie pomaga.

Pomocy: up

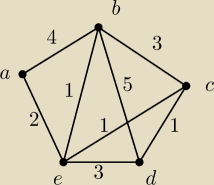
Pytający: Ekscentrycznością wierzchołka v nazywamy największą długość najkrótszej ścieżki wychodzącej z wierzchołka v. Łopatologiczniej: jeśli jesteś w wierzchołku v i masz tyle paliwa, żeby przejechać drogę długości równej ekscentryczności tego wierzchołka v, to na pewno jesteś w stanie na tym paliwie dojechać do któregokolwiek wierzchołka zechcesz. Pewnie wciąż niewiele to mówi, więc przykład przerysowany stąd: http://math.uni.lodz.pl/~bartkiew/tgis/tgis_11.pdf Odległości (najkrótsze ścieżki, zwroty strzałek nieistotne − graf nieskierowany): dist(a,b)=2+1=3 // a→e→b dist(a,c)=2+1=3 // a→e→c dist(a,d)=2+1+1=4 // a→e→c→d dist(a,e)=2 // a→e dist(b,c)=1+1=2 // b→e→c dist(b,d)=1+1+1=3 // b→e→c→d dist(b,e)=1 // b→e dist(c,d)=1 // c→d dist(c,e)=1 // c→e dist(d,e)=1+1=2 // d→c→e I teraz ekscentryczności: ex(a)=max{dist(a,b),dist(a,c),dist(a,d),dist(a,e)}=4 ex(b)=max{dist(a,b),dist(b,c),dist(b,d),dist(b,e)}=3 ex(c)=max{dist(a,c),dist(b,c),dist(c,d),dist(c,e)}=3 ex(d)=max{dist(a,d),dist(b,d),dist(c,d),dist(d,e)}=4 ex(e)=max{dist(a,e),dist(b,e),dist(c,e),dist(d,e)}=2

Pomocy: Pytający jesteś mistrzem! teraz dopiero rozumiem w jaki sposób się to liczy, bardzo dziękuje

Pytający: Bardzo proszę.