Przekątne w graniastosłupach Kasia S: Mam problem z zadaniem z geometrii. Jest takie zadanie: Podstawą graniastosłupa prostego jest trapez prostokątny, którego kąt ostry ma miarę 45 stopni. Dwie prostopadłe ściany boczne są przystającymi kwadratami. Krótsza przekątna graniastosłupa ma długość 2 √3 Oblicz sumę długości wszystkichkrawędzi tego graniastosłupa. Nie wiem jak rozwiązać to zadanie i proszę o pomoc Dziękuje

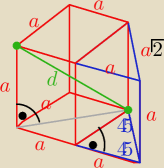
Eta: Taki graniastosłup składa się z sześcianu o krawędzi a i doklejonego graniastosłupa o podstawie trójkąta prostokątnego równoramiennego o przyprostokątnych długości a krótsza przekątna graniastosłupa to przekątna sześcianu d=a√3 =2√3 ⇒ a=2 Suma długości wszystkich krawędzi to: Obwód podstawy ( trapezu) =(2a+2a+a√2)*2 + długość czterech wysokości 4h ,h=a zatem s= 12a+2a√2= 24+4√2 [ j ] ====== Możesz też narysować siatkę tego graniastosłupa i zobaczysz s= (4a+a√2*2+4a =........