funkcje odwrotne 5-latek: Wyznaczyc funkcje odwrotna do danej funkcji (zbadac najpierw czy funkcja odwrotna w danym przykladzie istnieje ) mam do zrobienia 10 przykladow Oprocz nr 1 to wszystkie sa sklejane

	2x
1) f(x)=		f : (0,∞)→(0,2)
	1+x

D_f= R\{−1} Znam wykres tej funkcji i jest ona roznowartosciowa na tym przedziale i jest na Czy trzeba wykazac roznowartosciowsc ?

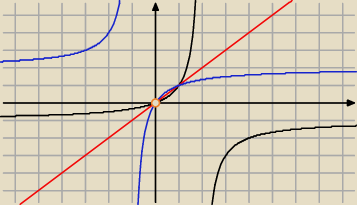
5-latek: to

	2x
y=
	x+1

y(x+1)= 2x yx+y=2x yx−2x=−y x(y−2)= −y

	−y
x=
	y−2

	−x
f−1(x)=
	x−2

Zgadzaloby sie

Jerzy: Cześć Ja bym tego nie robił.

5-latek: Witaj Teraz nr 2 f(x)= (x+4 dla x<0 (√x+4 x≥0 f : R→R Funkcja odwrotna do niej nie istnieje bo nie jest ona roznowartosciowa f(−1)=3 f(5)=3

Jerzy: Zgadza się.

5-latek: Nr 3 f(x)= ( x+1 x≤0 ( √x+7 x>0 f :R→ (−∞,1> U(7,∞) D_f= x≥−7 Ta funkcja jest roznowartosciowa i na Wobec tego istnieje funkcja do niej odwrotna y=x+1 i x≤0 to y≤1 −x= 1−y to x= y−1 f¹(x) = x−1 y= √x+7 i x>0 to y>0 y=√x+7 to y²= x+7 to −x= 7−y² to x= y²−7 f¹(x)= x²−7 Co mi program oszukuje wykresy wiec nie bede rysowal teraz Muszse tylko rysowac dla x≥−7?

Jerzy: Upewnij się co do zapisu zbioru wartośi, bo już widać,że funkcja nie ma wartości np. dla x = 1

Jerzy: Poza tym, dlaczego twierdzisz,że D_f = x ≥ −7 ?

5-latek: Taki jest dokladnie zapis Ale tez juz widze ze powinno byc chyba f : R→(−∞, 1>U(√7,∞) Miala byc ksiazka poprawiona a jednak bledy sa i tak

Jerzy: Wtedy to ma sens i popraw dziedzinę.

5-latek: Tak to jest jak sie stara liczyc w pamieci

5-latek: Na razie dziekuje za pomoc Za godzinke sie odezwe

5-latek: nr 4 f(x)= (−x dla x≤0 (√x dla x>0 f : R→<0 ,∞) y=−x i x≤0 to y≥0 y= √x i x>0 to y>0 wiec ta funkcja nie jest roznowartosciowa wiec nie ma funkcji odwrotnej

5-latek: nr 5 f(x)= √−x dla x≤0 x² dla x>0 f: R→<0, ∞) nr 6 f(x)= ln(−x) x<0 √x x≥0 Nie maja funkcj odwrotnej gdyz nie sa roznowartosciowe

Jerzy: Tak, np.: f(−1) = f(1) = 1

Jerzy: Podobnie w 5)

5-latek: nr 7 f(x)= x³ x≤0 √x x>0 f : R→R Istnieje funkcja odwrotna (mozna policzyc w pamieci dla x≤0 f⁻¹(x)= ³√x dla x>0 f⁻¹(x)= x² nr 8 ===== Tutaj bede mial problem f(x)= {−√−x x≤0 { 2√x x>0 f: R→R Istnieje do niej funkcja odwrotna gdyz y= −√−x dla x≤0 y≤0 y= 2√x dla x>0 y>0 Jak wyznaczyc funkcje odwrotna do y= −√−x ? do y= 2√x wiem

Jerzy: y = −√−x ⇔ −y = √−x ⇔ −x = (−y)² = y² ⇔ x = −y²

5-latek: i x≤0 dla tej czesci rysuje funkcje odwrotna Dobrze dziekuje Ci

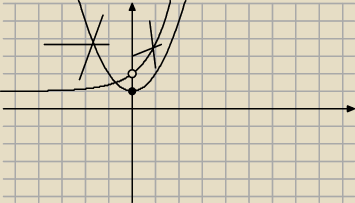
5-latek: nr 9 f(x)= {e^x+1 dla x<0 {x²+1 dla x≥0 f; R→(0,∞) ta funkcja nie bedzie miala funkcji odwrotnej gdyz nie jest roznawartosciowa Takze nie jest na gdyz zbior wartosci tej funkcji <1,∞) jest podzbiorem (0,∞)

Jerzy: Tak.

5-latek: Nr 10 tak samo nie jest roznowartosciowa Jerzy troche trudnosc mi sprawia bez wykresu okreslenie czy funkcja jest roznwartosciowa czy nie Bo takie tutaj jak te sklejane to najlepiej chyba wykresem ?

Jerzy: Tak, często szkic pomaga .

5-latek: dzieki za pomoc jeszcze raz na tym zakonczymy funkcje odwrotne . Teraz zabieramy sie za momotonicznosc funkcji

Jerzy: Tylko się nie zamomotaj

5-latek: Pewnie masz racje bo juz pierwsze definicje i wnioski i przyklad jakos intuicyjnie nie pasuja . ale napiszse w osobnym poscie