optymalizacja janusz-matematyki: Suma długości wszystkich krawędzi podstawy i wysokości ostrosłupa prawidłowego czworokątnego wynosi 4. Oblicz długość krawędzi podstawy dla której objętość ostrosłupa jest największa. Wyznacz tę objętość.

janusz-matematyki: .

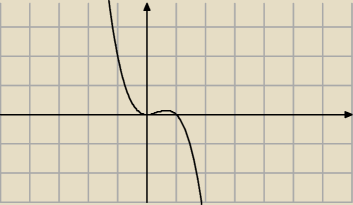
Mila: 4a+H=4 H=4−4a 4−4a>0 a∊(0,1)

	1		4
V(a)=		*a2*(4−4a)=		*(a2−a3)
	3		3

	4
V'(a)=		*(2a−3a2)
	3

2a−3a²=0 a*(2−3a)=0 2−3a=0

	2
dla a=		pochodna zmienia znak z (+) na (−) , zatem
	3

	2
V(a) ma maksimum dla a=
	3

janusz-matematyki: dzięki