rachunek prawdopodobieństwa, bernoulli Krzysztof1: Niech m, n będą dwoma liczbami całkowitymi dodatnimi, zaś 0 ≤ p,q ≤ 1; p + q = 1. Udowodnić wzór: (1 − pⁿ)^m + (1 − q^m)ⁿ ≥­ 1 . Jest to zadanie z rachunku prawdopodobieństwa, nie wiem jak się do niego niestety dobrać. Podejrzewam, że przydatny może być wzór ze schematu Bernoulliego lub jakieś jego pochodne, lecz nie wiem jak go zastosować. Bardzo proszę o pomoc.

jc: Rysujesz tablicę nxm. W każdym polu umieszczasz kreskę pionową lub poziomą (prawdopodobieństwa p i q). A oznacza, że ułoży się linia pionowa, B linia pozioma. AB=0 bo dwie linie na pewno się nie ułożą. P(A)=1−(1−pⁿ)^m P(B)=1−(1−q^m)ⁿ 1 ≥ P(A lub B) = P(A) + P(B) = 2 − (1−pⁿ)^m − (1−q^m)ⁿ Stąd (1−pⁿ)^m − (1−q^m)ⁿ ≥ 1.

Krzysztof1: Nie bardzo rozumiem tego jak mam narysować tą tablicę. Mógłbyś nakreślić choć kawałek? Ogólnie to dzięki bardzo za pomoc.

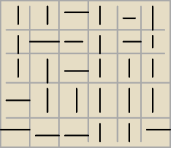
jc: W w czwartej kolumnie masz połączenie góra − dół. Oczywiście wyklucza to połączenie lewo − prawo.