Funkcja Mariusz: Wyznacz wszystkie wartości parametru m dla których równanie |x−4|+|2−x|=m ma dokładnie 2 różne rozwiązania dodatnie.

Mariusz: ?

Kacper: Graficznie proponuję

Janek191: I x − 4 I + I 2 − x I = m 1) x < 2 4 − x + 2 − x = − 2 x + 6 2) 2 ≤ x ≤ 4 4 − x + x − 2 = 2 3) x > 4 x − 4 + x − 2 = 2 x − 6 Dokończ

Mariusz: Właśnie sam zrobiłem do tego momentu. Dalej nie wiem co z tym zrobić..

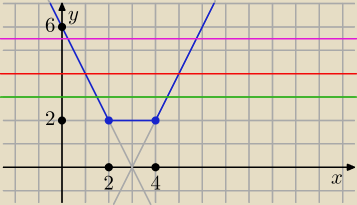
Janek191: Na osi OY odczytaj dla jakich y ( m ) proste y = m przecinają wykres funkcji f(x) = I x − 4 I = I 2 − x I dwukrotnie i x musi być wtedy > 0.

Mariusz: Nie wiem, chodzi o to, że m <2,6>?

5-latek: m∊<2.6) bo dla m=6 masz dwa rozwiazanie ale nieujemne

5-latek: Chociaz tutaj nasuwa sie takie pytanie czy dla m=2 mamy dwa rozwiazania dodatnie czy jedno czy nieskonczenie wiele dodatnich rozwiazan ? Nie wiem .

Mariusz: okej, dzięki

iteRacj@: witaj 5−latku, 2 nie należy do zbioru rozwiązań. dla m = 2 jest nieskończenie wiele rozwiązań, a to nie są dokładnie 2 różne rozwiązania dodatnie.

Janek191: m ∊ ( 2, 6) ==========

5-latek: Dobry wieczor iteracj@ i Janek191 Juz rozumiem

Janek191: Dobry wieczór