proszę o rozwiązanie Anna: wyznacz wszystkie wartości parametru m dla których równanie (4 + x)² = 24 −2m² ma dwa rozwiązania przeciwnych znaków 24 −2m² ≥ 0 ⇔ m² ≥ 12 ⇔ −2√3 ≥ m ≥ 2√3 czyli m ∊ ≤ −2√3 ; 2√3 ≥ czy to jest dobrze zad 2 sporządź wykres funkcji g(p) = liczba rozwiązań równania

4
	= p
IIxI − 2I

wykresem będzie hiperbola która jest w ćwiartce I i II ale nie wiem czy to jest dobrze

Jerzy: 1) Źle.

jc: 24−2m² > 16 m² < 4 m ∊ (−2, 2)

Anna: skąd liczba 16

PW: Zadanie 1. Bez "=", bo gdy (4+x)² = 0, to rozwiązanie jest tylko jedno. Ładny początek, bo bez nieśmiertelnej delty, ale to nie koniec. Nie rozstrzygnęłaś, dla jakich m te rozwiązania są przeciwnych znaków. Przykład. m = 2√2, prawa strona jest równa 8 − mamy równanie (4+x)² = 8, jego rozwiązania to x₁=√8−4<0 oraz x₂=−√8−4<0. ========= Powinno być w Twoim początku m²≤12, ale rozumiem że to błąd pisarski − dalej jest dobrze.

Anna: do zad 1 słusznie m² ≤ 12 czyli m ∊ ≤ −2√3 ; 2√3 ≥ czy na tym można zakończyć rozumowanie

Jerzy: Nie można, bo to tylko gwarantuje dwa rozwiązania, ale niekonicznie przeciwnych znaków.

jc: |x+4| to odległość x od −4. Liczby ujemne zawsze znajdziemy po lewej stronie, ale dodatnie leżą dopiero w odległości 4, a 4²=16.

PW: Wcześniej już pisałem, że nie może być po prawej stronie 0, a więc m² < 12, m ∊ (−2√3, 2√3). Bezmyślnie powtórzyłem Twój zapis. Przykład pokazuje, że nie można tu zakończyć, trzeba jeszcze obliczyć, dla jakich m rozwiązania są przeciwnych znaków..

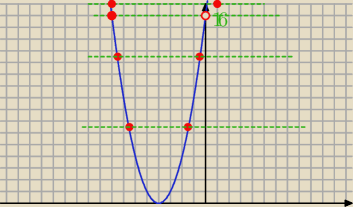
sinus: powyżej 16 czyli dla 24−2m²>16 −−− są 2 rozwiązania przeciwnych znaków ( jak napisał jc zatem dla m∊(−2,2)

Anna: (4 + x)² = 0 ⇔ 16 + 8x +x² = 0 dlaczego 24−2m² >16 na jakiej podstawie przyrównujemy do liczby 16

Jerzy: Anna, najwyraźniej komentarz jc jest dla Ciebie za trudny, ale popatrz na rysunek Ety, tam wszystko ładnie widać.

Jerzy: Ta zielona linia to prosta: y = 24 − 2m²

Anna: dziękuję a jak zad 2

Jerzy:

	4		4
|x| − 2 =		lub |x| = −		i teraz analizuj rozwiązania.
	p		p

PW: Albo "po szkolnemu". Mamy równanie (4+x)² = (√24−2m²)², m∊(−2√3, 2√3) 4+x = −√24−2m² lub x+4 = √24−2m² x = − 4 − √24−2m² lub x = −4 + √24−2m² Pierwsze z rozwiązań jest ujemne w sposób oczywisty, musimy więc zadbać, by drugie było dodarnie −4 + √24−2m² > 0, m∊(−2√3, 2√3) √24−2m² >4 m∊(−2√3, 2√3) − i teraz widać, co jc miał na myśli (ale Kolega jc jest błyskotliwy i nie zawsze widać od razu o czym mówi )

PW: Przecinka brakuje przed "m∊" w trzecim wierszu od dołu.

Anna: jeszcze raz dziękuję

Eta: Metoda graficzna też jest "po szkolnemu" i .......... jest najprostszą metodą !

PW: Tak , ale czasem człowiek się "zatnie" i nie rozumie, warto mieć w zanadrzu inny sposób.

Anna: natomiast w zadaniu 2 wiem jak narysować I x I − 2 ale nie bardzo wiem jak przeanalizować liczbę rozwiązań

	4		4
dla I x I − 2 =		lub I x I − 2 = −
	p		p

	4
bo		jest ułamkiem
	p

Jerzy:

	4
Nie szkodzi , tak jak poprzednio , tylko teraz twoja prosta y =
	p

Jerzy:

	4		4
Łatwiej Ci będzie: |x| =		+ 2 lub |x| = −		+ 2
	p		p

Jerzy:

Eta:

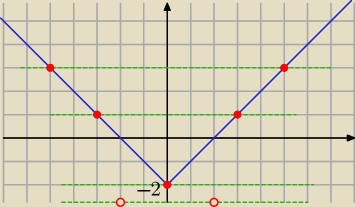
	−4
Zielone proste : y=		, p≠0
	p

	4
0 rozwiązań dla −		<−2 ⇒..............
	p

	−4
1 rozwiązanie dla		=−2 ⇒................
	p

	−4
2 rozwiązania dla		>−2 ⇒ .............
	p

Anna: po obliczeniu 0 rozwiązań dla p ∊( − ∞ ;2 ) 1 rozwiązanie dla p =2 2 rozwiązanie dla p ∊ ( 2 + ∞ ) czy dobrze zrozumiałam

Anna: jeszcze raz powracam do zadania

	−4
jeżeli y =		< −2 to po rozwiązaniu tej nierówności otrzymamy
	p

rozwiązanie takie jak w poście 5 lis 16:01 i według mnie nie jest zgodne z wykresem Eta 5 lis 15: 45

	4
a jeżeli y =		< −2 to
	p

to po obliczeniu

	4
0 rozwiązań dla		< −2 ⇔ p< − 2 ⇔ p ∊( − ∞ ;2 )
	p

	4
1 rozwiązanie dla		< −2 ⇔ p =2
	p

	4
2 rozwiązanie dla		< −2 ⇔ p > −2 ⇔ p ∊ ( 2 + ∞ )
	p

i według mnie to to jest poprawna odpowiedź a nie z postu 5 list 16:01 bardzo proszę o odpowiedź

Anna: bardzo przepraszam ale nie wiem kto wpisał posty 9 lis 09:52 09:42 to są nie moje wpisy i nie wiem jak tak mógł ktoś za mnie napisać jeszcze raz proszę aby nikt tak nie pisał pod moim adresem