Liczby zespolone Mleko: Cześć. B = {z ∈C: Re(z−i)² ≤ 0} Mam wyznaczyć na płaszczyznie zespolonej. Wychodzi mi x² − y² + 2y − 1≤0 Jak powyzsze rownanie przestawić jako równanie okregu?

Mleko: b

PW: A dlaczego uważasz, że to musi być okrąg? x² − (y−1)² ≤ 0 i różnica kwadratów.

Mleko: Dziękuje!

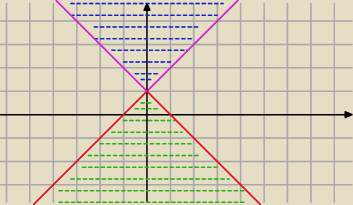
Mila: Re (z−i)²: z=x+iy, x−y∊R (x+iy−i)²=[x+i(y−1)]²=x²+2x(y−1)*i−(y−1)² Re(z−i)²=x²−(y−1)² x²−(y−1)²≤0⇔ I sposób x²≤(y−1)² |y−1|≥|x|⇔ y−1≥|x|⇔y≥|x|+1 punkty powyżej wykresu i na wykresie lub y−1≤−|x|⇔y≤−|x|+1 punkty poniżej wykresu i na wykresie II sposób (x−y+1)*(x+y−1)≤0 x−y+1≥0 i x+y−1≤0 lub (x−y+1)≤0 i (x+y−1)≥0 y≤x+1 i y≤−x+1 punkty poniżej prostych− część wspólna lub y≥x+1 i y≥−x+1 punkty powyżej prostych− część wspólna

Mleko: Dzieki Mila!

Mila:

5-latek: Zasadnicze pytanie Dlaczego chciales to przedstawic jako rownanie okregu skoro wiesz ze roznanie okregu jest takie x²+y²+A_x+B_y+C=0 ? Skoro ≤0 to kolo ale tez nie bo masz x²−y²