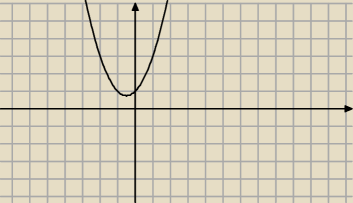
Typ na 5-latek: Mam kilka zagwozdek z funkcji typu (na) ma 12 funkcji do okreslenia czy sa (na) Tych ktorych nie rozumien podam po kolei f(x)= x²+x+1 f : R→R₊ Dlaczego ona jest nie na skoro dla kazdego x_sa z dziedziny wartosc funkcji jest dodatnia ? Taki sam problem z f(x)= e^x f : R→R₊

Janek191: Bo ZW ⊂ ℛ₊

5-latek: Dobry wieczor Janek191 Mozesz inaczej wytlumaczyc bo nie rozumiem .

Janek191: Aby była "na" , to musiało by być ZW = ℛ₊ Ta funkcja jest "w " ℛ₊

5-latek: Bo mam np taka funkcje

	x2
f(x)=		f : R→<0,1>
	1+x2

ta nie bedzie na bo nie osiaga wartosci 1 dla zadnego x_sa Mozna tamta wytlumaczyc jakos w ten sposob ? Wtedy pewnie zrozumie

Janek191: " na" tzn. na cały ℛ₊

5-latek: czyli (0,∞) ? no to e^x ma taki zbior wartosci

5-latek: Ok czyli f(x)= x²+x+1 Zw= <0,75,∞) czyli nie caly zbior R₊ (to rozumiem A co z y=e^x? (to wykladnicza i ZW= (0,∞) czyli caly R₊

Janek191: f(x) = e^x jest ℛ "na" ℛ₊

5-latek: czyli blad w ksiazce (a miala byc porawiona . Jeszce w sunie 3 funkcje f(x)= {e^x x≤0 {x⁴+2 x>2 f: R−(0,2> →R₊ czy narysowac wykres ? Ma byc nie na

Janek191: Czy dobrze przepisałeś ?

Janek191: Z wykresu widać, że nie jest "na".

5-latek: Tutaj nie bedzie zbiorem wartosci tej funkcji R₊ bo e⁰ =1 a x=0 jest wyrzucone z dziedziny tej funkcji wiec y−1 odpada z ezbioru wartosci tej funkcji Dobrze ?

5-latek:

Jerzy: Jeżeli: f : R →R , to funkcja y = x² jest "w" Jeżeli: f: R → [0;+∞) , to funkcja y = x² jest "na"

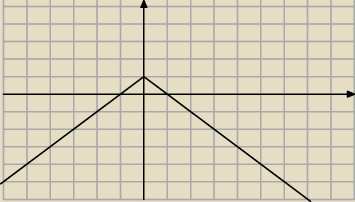
5-latek: To rozumiem Teraz mam taka funkcje f(x)= −|−x|+1 f : R→(−∞,−1> Funkcje f(x) moge zapisac f(x)= −|x|+1 czyli nie cale odwzorowanie miewsci sie w zbiorze wartosci funkcji f(x) czyli funkcja nie jest na , Dobrze to jest ?

Jerzy: Jest "na" , bo przeksztalca R→ (−∞;1]

5-latek: Jerzy ma byc (−∞ −1>

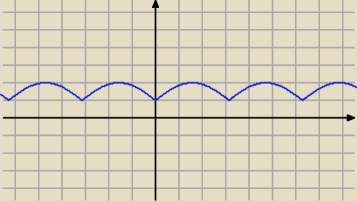
5-latek: f(x)= |xin(x)|+1 f:R→(−0,5 ∞) Ta funkcja nie jest na Bylaby na gdyby bylo odwzorowanie <1,2>

5-latek: Ostatnia funkcja f(x)= √sin²x−1 f : D_f →{0} ta funkcja jest na

5-latek:

iteRacj@: ostatnia funkcja jest "na" ale ciekawa jestem dlaczego napisałeś f(x)= −|−x|+1 f : R→(−∞,−1>

5-latek: Dobry wieczor taka zapisana jest funkcja w ksiazce

iteRacj@: tak jak Jerzy napisał, zbiór wartości funkcji to R→ (−∞;1>. Nie rozumiem skąd −1, może ktoś to wytłumaczy

5-latek: Wiec tak jak napisalem nie bedzie na W odpowiedzi mam tez ze nie jest na Tylko czy moje wytlumaczenie jest dobre ?

iteRacj@: nie wiem, dziś już nic nie wymyślę

5-latek: Dobrze

jc: Dobry wieczór 5−latku. Chodzi o ten przykład f : R→(−∞,−1>, f(x)= −|x|+1 ? Pominąłem minus przy x, bo nie ma znaczenia. To jest niepoprawnie określona funkcja, bo f(0)=1, a liczba 1 nie należy do zbioru (−∞,−1).

5-latek: Dobry wieczor jc czyli tak jak myslalem .

jc: To w ogóle nie jest funkcja.

jc: Tak przy okazji, czy w książce, z której bierzesz zadania, powiedzieli, co to jest funkcja?

5-latek: Tak ja zapisal Pan dr z SGH a moze teraz juz profesor bo ksiazka z 2001r

5-latek: Tak jest napisane

5-latek: jest tak Niech X ,Y beda dowolnymi zbiorami Definicja Mowimy z e na zbiorze X zostala okreslona funkcja f o wartosciach w zbiorze Y (zapisujemy symbolicznie f:X→Y) jesli dla kazdego elementu x∊X zostal przyporzadkowany w sposob jednoznaczny pewen element y∊Y Elelemnt y∊Y przyporzadkowany elementowi x∊X oznaczamy y=f(x) Podkreslny jeszcze raz ze zapis f : X→Y oznacza : f odwzorowuje (przeksztalca ) zbior X w zbior Y Zamiast okreslenia funkcja czesto uzywamy zamiennie okreslenia odwzorowanie . Tyle jest napisane

jc: W niektórych podręcznikach piszą, że funkcja to podzbiór f ∊ XxY taki, że dla każdego x∊ X, znajdziemy dokładnie jedno y∊Y takie, że para (x,y) ∊ f. Zamiast (x,y) ∊ f, piszemy y=f(x). To jest to samo tylko inaczej powiedziane. Powyższa definicja utożsamia funkcję z wykresem.