Wyznaczyć dziedzinę i zbiór wartości funkcji Zdzisław: Wyznaczyć dziedzinę i zbiór wartości funkcji

	1−|x|
f(x)=2arcsin(		)
	2

Df :

	1−|x|
−1≤		≤1
	2

	1−|x|
1o		≥−1 ⇒ x∊<−3;3>
	2

	1−|x|
2o		≤1 ⇒ x∊R
	2

Df= <−3;3> Jak mam obliczyć zbiór wartości?

Jerzy: A widziałeś kiedyś wykres funkcji f(x) = arcsinx ?

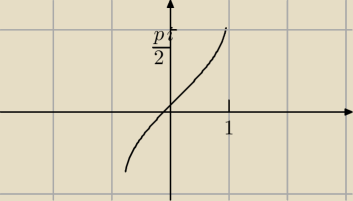
Zdzisław: zostały nam wytłumaczone bardzo słabo...

Jerzy: Czyli zbiór wartości: [ −π/2;π/2] , a zatem 2*arcsinx ma jaki zbiór wartości ?

3Silnia&6: funkcja arcsin(x) jest rosnaca, wiec minimalna wartosc przyjmnie dla najmniejszej wartosci, a najwieksza dla najwiekszej.

	1−|x|
dla		wartosc najmniejsza dla x ∊ [ −3, 3] to −1 (dla x = +/− 3 )
	2

	1−|x|
		wartosc najwieksza dla x ∊ [ −3, 3] to 1/2 (dla x = 0 )
	2

W_f = [ f(−1), f(1/2) ] = [−π, π/3]

Zdzisław: 2*arcsinx ma zbiór wartości [ −π/2 * 2 ; π/2 * 2] czyli [−π ; π] zgadza się?

3Silnia&6: zgadza sie zbior wartosci 2arssinx to [−π,π] ale zbior wartosc 2arcsin((1−|x|)/2) to [−π, π/3]

Zdzisław: Wartość najmniejszą dla x= +/− 3 rozumiem bo podstawiam krańce przedziałów ale nie wiem skąd wzięła się wartość największa 1/2 dla x=0. skąd wziąć te 0?

Jerzy:

	1 −|x|		1
Zauważ,że ułamek		osiąga mksymalna warość:		, dla |x| = 0
	2		2

3Silnia&6: jak pewnie pamietasz wyrazenie |x| przyjmuje tylko wartosci nieujemne (|x| ≥ 0 )

1−|x|		1		|x|
	=		−		← najwieksza wartosc jezeli odejmniemy najmniej ile sie da,
2		2		2

czyli 0 Wiec najwieksza wartosc jest w 0

Zdzisław: a da sie zrobic innym sposobem zamiast wyznaczac wartosci minimalne i maksymalne?

Zdzisław: ahhh teraz wszystko jasne co do tego, kwestia zapisu zmienia wszystko