Ciąg rekurencyjny Ivona: Dany jest ciąg rekurencyjny x₁=a; x_n+1=x_n(2−x_n), n≥1. W zależności od parametru a zbadaj, czy ciąg (x_n)_n∊N ma granicę. Jeśli tak, to podaj ją, wraz z uzasadnieniem.

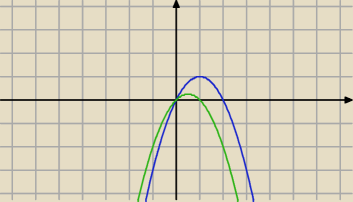
Adamm: rysujesz sobie 2 wykresy y=x(2−x) (niebieski) oraz y=x(2−x)−x (zielony) zielony wykres przedstawia jak ciąg się zachowuje jeśli chodzi o monotoniczność niebieski, jak się zachowuje jeśli chodzi o wyrazy ciągu widać że mamy 2 punkty stałe dla a=0 oraz a=1 dla a∊(−∞;0) ciąg stale maleje w dodatku, maleje coraz szybciej, więc na pewno będzie dążył do −∞ dla a∊(1;∞) ciąg również stale maleje, ale nie możemy za dużo powiedzieć dla x∊(1;2), 1>x(2−x)>0, więc od drugiego wyrazu będziemy mieli sytuację a∊(0;1) dla x∊(2;∞) x(2−x)<0, i od drugiego wyrazu mamy sytuację a∊(−∞; 0) pozostało sprawdzić co dla a∊(0;1) 0<x(2−x)<1 więc ciąg jest ograniczony, ale również, cały czas rośnie, więc będzie dążył do skończonej granicy ta granica musi być oczywiście punktem x=1 (dla pewności można przejść do granicy w równaniu x_n+1=x_n(2−x_n) i mamy g=g(2−g) skąd g=1 lub g=0)

Adamm: aha jeszcze dla a=2 mamy ciąg stały od drugiego wyrazu