wartość bezwzgledna w mianowniku i liczniku gość: mam taką nierówność: |^x−1_x|≤2 zamieniam na taką korzystając z własności nierówności. ^|x−1|_|x|≤2 rozwiązuję 4 przypadki, kiedy 1) x−1≥0 x>0 2) x−1≥0 x<0 3) x−1<0 x>0 4) x−1<0 x<0 i w pierwszym wychodzi mi: x∊(−∞;−1> u (0,+∞) drugim: x∊(−∞;0) u <3,+∞) trzecim: x∊(−∞;0> u (¹₃,+∞) czwartym: x∊(−∞;−1> u (0,+∞) gdzie popełniam błąd? jak mam rozważać te x względem przedziałów które rozpatruje? W sensie mam np. x≥1 i jednoczesnie x<0 wiec co robić?

5-latek: Mozesz skorzystac z wlasnosci (ogolnej |x|≤a ⇔x≤a lub x≥−a

5-latek: czyli dla x≠0

x−1		x−1
	≤2 i		≥−2
x		x

Szybciej i prosciej niz rozpisywanie modulow

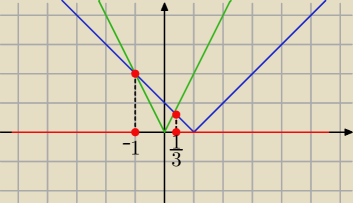
Eta: x≠0 |x−1|≤2|x| x−1≤2x i x−1≥−2x ⇒ x∊(−∞, −1> U <1/3, ∞) ====================

PW: Ja bym to zrobił tak:

	x−1
|		| ≤ 2
	x

	x−1
−2 ≤		≤ 2
	x

	1
−2 ≤ 1 −		≤ 2
	x

	1
−3 ≤ −		≤ 1
	x

	1
−1 ≤		≤ 3
	x

− i po co to żmudne "rozbijanie na przedziały"?

5-latek: taka mala uwaga do tego co napisales Nie z wlasnosci nierownosci korzystajac tylko z wlasnosci wartosci bezwzglednej Teraz dalej dla x≠0 mozemy pomnozyc obie strony nierownosci przez |x| bo |x| jest zawsze dodatnia i nie zmienimy zwrotu nierownosci Masz wtedy |x−1|≤2|x| teraz przedzialy x−1=0 to x= 1 1) (−∞,0) 2) (0,1> 3) (1∞) na tych przedzialach rozwiazujesz te nierownosc

Jerzy: PW , ale : x ≠ 0

Jerzy: Witaj Eta...z armatą na wróble ?

PW: Założyłem, że pytający to widzi , bo tak pisał w pierwszym poście.

Jerzy: Racja, nie dopuszcza: x = 0

Eta: Hej Jerzy Tu nie ma "armaty"

gość: Rozumiem sposób użytkownika Eta ale chcąc uniknąć wykresów próbuję sposobu PW: 1) ^x−1_x≤2 x−1≤2x x−2x−1≤0 x≥−1 2) ^x−1_x≥−2 x−1≥−2x x−1+2x≥0 3x≥1 x≥¹₃ gdzie popełniam błąd?

iteRacj@: rozwiązujesz inaczej niż PW nierówność mnożysz stronami przez niewiadomą, a o niewiadomej nie wiadomo, czy jest dodatnia czy ujemna dla ujemnej trzeba zmieniać zwrot nierówności... dlatego dostajesz inny wynik

gość: dobrze a mnożąc przez x²? mogę tak zrobić?

iteRacj@: możesz pomnożyć przez x², dostaniesz równania kwadratowe, trzeba sprawdzić, czy będzie prościej je rozwiązać masz powyżej proste sposoby i koniecznie pamiętaj, że x=/=0, bo zero trafiło do Twoich rozwiązań

iteRacj@: miało być nierówności kwadratowe

gość: no dobrze ale wtedy z nierówności kwadratowych wychodzi mi: 1) x∊(−∞;−1> u (0,+∞) 2) x∊(−∞;0) u <¹₃;+∞) to dlaczego odrzucam przedziały (0,+∞) i (−∞;0) ?

Jerzy: Pokaz jak ty to robisz .

gość: 1)^x−1_x≤2 (1−1)x≤2x² −x²−x≤0 −x(x+1)≤0 rysuje wykres i wychodzi mi taki przedzial jak poprzednim poście. 2)^x−1_x≥−2 (x−1)x≥−2x² 3x²−x≥0 3x(x−¹₃)≥0 wykres i przedzial jak wyżej.

gość: podbijam

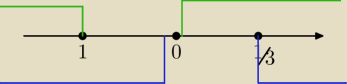
Jerzy: Potrafisz wyznaczyć część wspónną tych zbiorów ?

gość: No tak, ale dlaczego to ma być część wspólna? A nie suma?

gość: skoro obliczam x w różnych przedziałach, czyli x może być "taki lub taki lub taki", to zawsze brałem sumę. Część wspólną brałem kiedy x miał być jednocześnie "taki i taki"

Jerzy: Wiesz co to jest koniunkcja ?

gość: no tak, ale przy rozwiazywaniu wartosci bezwzglednych mamy alternatywe?

Jerzy: W tym przypadku koniunkcja. |a| > A ..... tutaj alternatywa.