Zbiory liczby zespolone
norbi: Witam mam za zadanie naszkicować zbiory liczb zespolonych i mam jeden problem z przykładem
Rozwiązuje to tak:
|z+3| = |z−2i| − Teraz za z podstawiam z = x + iy
|x+iy+3| = |x+iy−2i|
√(x+3)2 − y2 =
√x2 + (y−2)2 − Obie strony podnoszę do kwadratu
(x+3)
2 − y
2 = x
2 + (y−2)
2
x
2 + 6x + 9 + y
2 = x
2 + y
2 − 4y − 4
6x + 4y = −5
W tym momencie nie wiem co zrobić, mógłby mnie ktoś naprowadzić co robię źle albo jak można
dalej to rozpisać?
3 lis 17:36
janek: Łatwiej jest chyba bezpośrednio graficznie.
|z+3|=|z−2i|
|z−(−3)|=|z−2i|
Czyli szukasz liczb zespolonych, których odległość od −3 jest taka sama jak odległość od 2i,
będzie to symetralna odcinka o końcach w punkcie −3 i 2i
3 lis 17:39
janek: z tego co ty liczyłeś, to poprostu wychodzi, że trzeba narysować prostą o równaniu 6x+4y=−5
3 lis 17:40
Dzik: Jak już masz tak rozpisane (zakładając że jest to dobrze wyliczone, bo nie sprawdzam

) to
możesz to przekształcić to wzoru
4y = −6x −5
y = −
64x−
54
a więc
y = −1.5x −1.25
i masz już zwykłą prostą
3 lis 17:44
norbi: Janek i Dzik − Bardzo wam dziękuje, po prostu nie myślałem, że rozwiązaniem będą wszystkie
liczby zespolone leżące na tej prostej i spodziewałem się czegoś innego przez co tego nie
zauważyłem. Dziękuj bardzo za pomoc

3 lis 17:49
janek: 
3 lis 17:51
norbi: Janek Żeby nie zakładać już nowego tematu to spytam jak można rozwiązywać takie zadania
sposobem bez podstawiania? Rozumiem, że skorzystałeś tu z tego, że |z1 − z2| to odległość
między tymi liczbami.
Jak by można było rozwiązać tym sposobem następujący przykład?
|z2+4| <= |z−2i|
3 lis 18:32
Mila:
⇔
|z
2−4i
2|−|z−2i|≤0⇔
|z−2i|*|z+2i|−|z−2i|≤0
|z−2i|*(|z+2i|−1)≤0
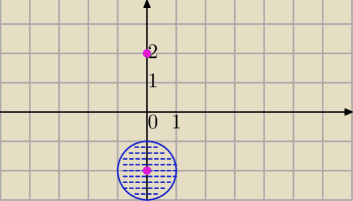
|z−2i|=0 lub |z+2i|≤1
z=2i lub |z−(−2i)|≤1 koło o środku (0−2) i r=1
3 lis 18:46
norbi: Dziękuje ślicznie

3 lis 18:55
Mila:

3 lis 19:14
 ) to
możesz to przekształcić to wzoru
4y = −6x −5
y = −64x−54
a więc
y = −1.5x −1.25
i masz już zwykłą prostą
) to
możesz to przekształcić to wzoru
4y = −6x −5
y = −64x−54
a więc
y = −1.5x −1.25
i masz już zwykłą prostą


 ⇔
|z2−4i2|−|z−2i|≤0⇔
|z−2i|*|z+2i|−|z−2i|≤0
|z−2i|*(|z+2i|−1)≤0
|z−2i|=0 lub |z+2i|≤1
z=2i lub |z−(−2i)|≤1 koło o środku (0−2) i r=1
⇔
|z2−4i2|−|z−2i|≤0⇔
|z−2i|*|z+2i|−|z−2i|≤0
|z−2i|*(|z+2i|−1)≤0
|z−2i|=0 lub |z+2i|≤1
z=2i lub |z−(−2i)|≤1 koło o środku (0−2) i r=1

