Czy to dobry sposób rozwiązania zadania? ralf: Wyznacz wszystkie wartości parametru m, m∊R, dla których równanie z niewiadomą x, 3|x−3|=12,−4m² ma dwa (różne) rozwiązania dodatnie.

	4		4
Przekształcając równanie otrzymuję |x−3|=4m −		m2, więc x1=4m −		m2+3 i x2=
	3		3

	4
−4m+		m2+3
	3

Ja bym postawił takie warunki: (x₁ i x₂)>0 i x₁≠x₂,

	3		3−3√2		3+3√2
wyszło by wtedy m≠		(dla x2>0, m∊(		;		) (dla x1>0) i m≠0 i m≠3(z
	2		2		2

	3		3
założenia x1≠x2), lecz w odpowiedziach jest po prostu m∊(0;		)U(		;3) i nie mam
	2		2

pojęcia czy czegoś jeszcze nie uwzględniłem czy może mam jakiś błąd

kochanus_niepospolitus: wyjściowe równanie to 3|x−3| = 12m − 4m²

ralf: Tak, jestem też niemalże pewny że nie jest to błąd w książce

ralf: Nie zauważyłem że chodzi o to że napisałem tam przecinek. @kochanus_niepospolitus tak, rówanie to 3|x−3|=12m−4m²

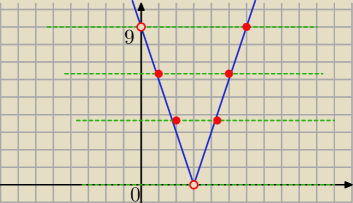Eta: 2 rozwiązania dodatnie są gdy 0<12m−4m²<9 4m²−12m<0 i 4m²−12m+9>0 m(m−3)<0 i (2m−3)²>0 m∊(0,3) i m∊(−∞,3/2)U (3/2,∞) Odp m∊(0,3/2) U(0,3) ===============

Eta: f(x)= 3|x−3| y=12m−4m²

Eta: Poprawiam chochlika m∊(0,3/2) U (3/2, 3)

ralf: Dziękuję @Eta za rozwiązanie, jest ono jasne dla mnie, lecz chciałbym jeszcze dowiedzieć się co u mnie jest źle zrobione, żeby na przyszłość uważać na to

ralf: Ktoś coś jeszcze pomoc w moim pytaniu ?

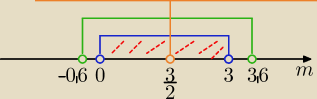
Eta: 1/ aby to równanie miało dwa rozwiązania to 12m−4m²>0 ⇒ m∊(0,3) 2/ aby obydwa rozwiązania były dodatnie

	4		4
to 4m−		m2+3>0 i −4m+		m2+3>0
	3		3

4m²+12m−9<0 i 4m²−12m+9>0

	3−3√2		3+3√2
m∊(		,		) ≈ m∊(−0,6; 3,6)
	2		2

i m∊ (−∞.3/2)U(3/2,∞) Po wybraniu części wspólnej otrzymujemy Odp: m∊(0,3/2) U (3/2,3) ================ W tego typu zadaniach najprostsza jest metoda graficzna, którą podałam w poprzednim poście