Proszę o pomoc :) Kasia10953: Zbadaj monotoniczność i ograniczność ciągu an=cos1/n

kochanus_niepospolitus: Ograniczony jest z wiadomego względu, którego chyba nie trzeba nawet podawać, do studentka o tym doskonale wie.

	1
Co do monotoniczności ... należy zauważyć, że		−> 0 więc cos(1/n) będzie .....
	n

Kasia10953: Nie rozumiem o co chodzi Tobie z tą monotonicznośścią Czy mógłbyś mi bardziej szczegółowo wytłumaczyć?

kochanus_niepospolitus: Ale czego konkretnie 'z tą monotonicznością' nie rozumiesz? Nie wiesz co to jest monotoniczność ciągu czy co Znasz wykres f(x) = cosx

Kasia10953: Tak znam ten wykres

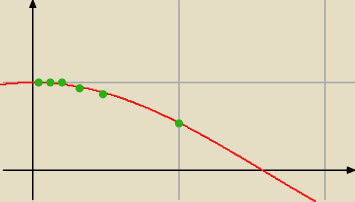
kochanus_niepospolitus: No to rysujemy sobie wykres f(x) = cosx

	1
dla n=1 ...		= 1
	n

zaznaczamy cos 1 (1 to jest LICZBA To nie jest kąt )

	1		1
dla n=2 ...		=
	n		2

itd. Widzimy, że idziemy coraz bliżej osi OY (czyli x=0), a wartość funkcji f(x) = cosx jest coraz większa. Wniosek: ciąg a_n = cos(1/n) jest ciągiem rosnącym

PW: Kasiu, policz a_n+1−a_n wzorem na różnicę kosinusów, może coś wyjdzie (dodatniego lub ujemnego).

yht: no to jak się zachowują wartości cosinusa, gdy jego argument zmniejszamy stopniowo do zera ? cos(50⁰) = ? cos(40⁰) = ? cos(30⁰) = ? cos(20⁰) = ? cos(10⁰) = ? cos(9⁰) = ? ... cos(1⁰) = ? cos(0,5⁰) = ?

Kasia10953: Dziękuję bardzo z an pomoc

Kasia10953: Dziękuję bardzo z an pomoc