Ciag rekurencyjny- ograniczonosc Olis: Ja wykazać ograniczonosc tego ciągu a₀= 1 , a_n+1=(3 + 2 a_n)/ (3+a_n) ? Próbowałam intuicyjnie ale nie wiem jak ograniczyć licznik i mianownik gdzie jest a_n

Olis: Indukcyjnie*

PW:

3+2an		an
	= 1+
3+an		3+an

Ułamek jest mniejszy od 1 (bo licznik i mianownik dodatnie, a licznik mniejszy niż mianownik).

Olis: Dziękuję

Olis: A monotonicznosc?

PW:

	3+2ak		3+2ak−3ak+a2k
ak+1 − ak =		− ak =		=
	3+ak		3+ak

	a2k−ak+3
=		> 0
	3+ak

(mianownik dodatni i licznik dodatni, bo Δ<0). Pokazaliśmy, że dla wszystkich k≥0 a_k+1 − a_k > 0, a więc ciąg jest rosnący.

Olis: Dziękuję pieknie!

PW: Korekta. Błąd w odejmowaniu, powinno być

	−a2k−ak+3
	3+ak

W liczniku Δ=1+12 = 13, a więc nie tak łatwo! Spróbuj sama rozstrzygnąć jak to będzie, badając znak funkcji wymiernej

	−x2−x+3
	x+3

Olis: Niestety wkradł się błąd chyba ze znakiem przy an² I już nie wychodzi tak pięknie

Olis: Spróbuję moze z pochodnych wyjdzie

Olis: Nie wychodzi wychodzi że jest malejąca a nie rosnacy

PW: Spróbuj tak jak w szkole średniej: iloraz ma taki sam znak jak iloczyn, czyli zbadaj znak (−x²−x+3)(x+3) (rozłóż funkcję kwadratową na czynniki i rysuj "węża").

Olis: Wychodzi że większy od zera dla od −4,1... do −3 oraz od 1,302..... do nieskonczonosci

Olis: Chyba że należy sprawdzić kilka początkowych wyrazów do liczby 1.302... A potem napisac ze rosnący dla większych wyrazow

kochanus_niepospolitus: Jeżeli sprawdzisz kolejne wyrazy tego ciągu do 6 miejsc po przecinku to wyjdzie Ci bardzo szybko, że 'dojdziesz do granicy monotoniczności' i ciąg z rosnącego zmieni się na malejący (okolice 6−8 wyrazu tego ciągu). W efekcie − ciąg ten nie jest monotoniczny

Olis: Spróbuję sprawdzic

kochanus_niepospolitus: a jednak nie ciąg ten jest rosnący a granicą jest 1.30277653773199

kochanus_niepospolitus: w przybliżeniu

Olis: Niestety ciąg w tych wyrazach ciągle rośnie

Olis: Tylko jak pokazać że jest rosnący stale

kochanus_niepospolitus: tak jak napisałem

PW: Rysowałaś tego "węża"?

Olis: Rysowalam ale nic z tego sensownego nie wyszlo

kochanus_niepospolitus: PW ... wężyk nic Ci nie da ... ciąg zacznie maleć dopiero 'po przebiciu' granicy, a to jest ciąg rosnący do tejże właśnie granicy

	1
musimy wykazać, że ciąg ten jest ograniczony przez swoją granicę: g =		(√13 − 1)
	2

Olis: A co to da?

kochanus_niepospolitus: Jeżeli pokażemy, że ciąg a_n posiada granicę 'g' oraz a_n < g dla dowolnego 'n' to wiemy, że ciąg ten jest rosnący

Oliwka: wiem jak pokazac ze ma taka granice tylko jak udowodnic ze wszytkie wyrazy mniejsze od tej grancy tworza ciag rosnący

kochanus_niepospolitus: Jeżeli pokażesz, że wszystkie wyrazy ciągu a_n są mniejsze od 'g' ... a g jest ich granicą, to ... musi to być ciąg rosnący przynajmniej od jakiegoś N

PW:

	−1−√13		−1+√13
−(x2+x−3)(x−(−3)) = −(x−		)(x−		) (x−(−3))
	2		2

Dwa miejsca zerowe są ujemne, jedno dodatnie. Dla jakich x ten iloczyn jest dodatni? Interesują

	5
nas prawdę mówiąc tylko x >
	4

kochanus_niepospolitus:

	1
PW ... wszystkie x <		(√13 − 1) = g
	2

tyle, że jak pokazać, że a_n < g dla dowolnego n

Oliwka: Wyszlo że x musi być mniejsze od (√13−1 )*1/2 zeby to wszystko było dodatnie

Oliwka: no własnie ....

PW: Artur, po co mówić o g, jeżeli mamy udowodnić monotoniczność? Ja już pasuję, muszę odejść od ekranu, bo przestaję widzieć.Oliwka, analizuj węża z 12:41.

Oliwka: Przeanalizowałam go i wychodzi ze wyrazy an musza być mniejsze od (√13−1)*1/2 zeby znak był wiekszy od zera i a_n+1/a_n było >0

Oliwka: A skoro przeprowadze dowód ze nie ma wyrazów wiekszych od (√13−1)*1/2 bo jest to granica tego ciagu to znaczy ze wszystkie wyrazy do tej granicy beda rosnace zatem ta granica istnieje

Oliwka: Coś takiego wystarczy?

kochanus_niepospolitus: Tak ... problem w tym, że to musisz wykazać (że a_n < g dla dowolnego n)

Kinga: to tak sie chyba nie da...

kochanus_niepospolitus: Wiem. Zróbmy to tak: Dowód niewprost. Załóżmy, że istnieje takie k, że: a_k < g ∧ a_k+1 > g

	3 + 2ak		3+2g		3 + √13 − 1
ak+1 =		<		= 2*		=
	3+ak		3+g		6 + √13 − 1

	2 + √13		(2+√13)*(5−√13)
= 2*		= 2*		=
	5 + √13		25 − 13

	10 + 3 √13 − 13		3√13 − 3		√13 − 1
= 2*		=		=		= g
	12		6		2

sprzeczność W tym momencie wykazaliśmy, że o ile a_k < g to a_k+1 < g (to jest dowód indukcyjny, ale rozpisałem tylko już pkt 3 tylko)

kochanus_niepospolitus: w sumie to nie trzeba było niewprost Tylko indukcja: 1) n =1 a₁ = 1 < g 2) n = k a_k < g 3) n = k+1

	3 + 2ak		3 + 2g
ak+1 =		< // z (2) // <		= ... (reszta jak wyżej)
	3 + ak		3 + g

Kinga: Dziękuję

zombi: Te zadania są bardzo podobne. Dany jest ciąg rekurencyjny, a my pokazujemy że ma granicę zazwyczaj jednym sposobem: 1. Znajdujemy indeks, od którego ciąg jest stale monotoniczny 2. Pokazujemy ograniczoność ciągu 3. Wnioskujemy na podstawie twierdzenia z analizy 1, że ciąg ograniczony i monotoniczny jest zbieżny Dwa pierwsze kroki zazwyczaj wychodzą prosto. Monotoniczność nie powinna sprawiać problemu. Ograniczoność, tutaj pewna subtelność ze znajdowaniem ograniczenia (w końcu cała analiza to szacowanie ). Zakładamy ad hoc, że ciąg ten jest zbieżny, aby znaleźć granicę (najlepsze ograniczenie dla ciągu monotonicznego). Sprawa się komplikuje, jeśli ciąg zadany rekurencyjnie oscyluje i raz maleje raz rośnie lub ciężko znaleźć indeks od którego jest monotoniczny. Wtedy z pomocą przychodzi tw. Banacha o punkcie stałym, ale to inna beczka.

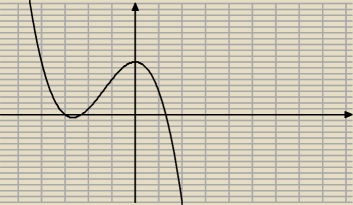
PW: Tak wygląda przebieg iloczynu. Dodatnie miejsce zerowe to

	1+√13
		> 4,1.
	2

Dla x∊(0,4) iloczyn jest dodatni. A w pierwszej części zadania pokazaliśmy, że wyrazy ciągu są mniejsze od 2, czyli nasze iksy (wyrazy ciągu) to liczby dodatnie mniejsze od 2.

PW: No i tu też błąd rachunkowy,

	1+√13
		> 2,3
	2

zachciało mi się kalkulatora zamiast policzyć w pamięci. Nie zmienia to na szczęście sensu oszacowania.

kochanus_niepospolitus: PW .... miejsca zerowe to: −3

	1+√13
−
	2

√13−1
2

kochanus_niepospolitus:

	√13−1
Natomiast		≈ 1.30277653773199
	2

kochanus_niepospolitus: Zresztą spójrz na swój wykres ... od razu widać, że dodatnie miejsce zerowej jest w przedziale (1 ; 2) (i to bliżej 1 niż 2).

kochanus_niepospolitus: Teraz już widzisz problem przy określaniu monotoniczności i widzisz czemu cały czas (jak ten

	√13 − 1
jelonek) odwoływałem się do g =
	2

kochanus_niepospolitus: zombi ... ale właśnie w tym zadaniu problemem było właśnie wskazanie czy ciąg jest monotoniczny

PW: No i jeszcze raz, mam dzisiaj "dzień głupiego". Ten dodatni pierwiastek to

	−1+√3
		> 1,3.
	2

Znowu nie jest tak łatwo jak się wydawało. Trzeba pokazać, że wyrazy ciągu są ograniczone przez np. 1,3,,to znaczy

	ak
		< 0,3,
	3+ak

czyli a_k < 0,9 + 0,3a_k 0,7a_k < 0,9

	9
ak <		.
	7

PW: Marna to pociecha, że w końcu do tego doszedłem. Wracamy do początku − jak oszacować a_k − już nie tak prymitywnie że mniejszy od 2.

kochanus_niepospolitus: PW ... Twoje ograniczenie jest zbyt 'ostre' (9/7 = 1,2857...) i już a₃ nie spełnia tego wymagania

kochanus_niepospolitus: PW −−− i teraz dochodzisz do : 12:24 (co jest wnioskiem z 11:25), a następnie do 13:16 i 13:14 I masz monotoniczność tego ciągu

jc: Inne spojrzenie. Narysujmy wykres y = x²+x−3. Na wykresie leży punkt (2,3) oraz punkt (1,−1) = (a₀,−1). Odcinek łączący punkty (2,3) i (a₀,−1) przecina oś poziomą w punkcie (a₁,0). Ogólnie: odcinek łączący punkty (2,3), (a_n, a_n²+a_n−3) przecina oś poziomą w punkcie (a_n+1, 0). Z rysunku wynika, że ciąg a_n jest rosnący ograniczony z góry przez większy z pierwiastków równania x²+x−3=0. Pierwiastek ten jest granicą ciągu. KONICZNY jest rysunek, a mam jakiś kłopot z rysunkiem. Może komuś się uda umieścić odpowiedni rysunek.

Blee: JC problem w tym ze to nie jest dowod na to ze a_n nigdy nie przebije granicy g i co za tym idzie, ciag nie przestanie byc rosnacym

Blee: Druga sprawa ... roznice pomiedzy kolejnymi wyrazami tego ciagu sa tak niewielkie, ze na rysunku nic bys nie zobaczyl.

jc: Blee. Zrobiłeś rysunek? Tak, to nie jest dowód. Ale rysunek jest o tyle lepszy, że w rachunkach można się pomylić. Poza tym rysunek wyjaśnia, jak tworzy się takie przykłady (a takich tajemnic nauczyciele zwykle nie zdradzają). Czy nie widzisz, że punkt przecięcia odcinka łączącego punk na paraboli powyżej osi poziomej z punktem leżącym na paraboli poniżej osi poziomej przecina oś poziomą pomiędzy pierwiastkami?

jc: Odpowiedź na drugą uwagę. To bardzo dobrze. Oznacza to, że ciąg jest szybko zbieżny (to jest metoda siecznych). Istnieje znacznie lepszy sposób (metoda stycznych).