Funkcja wymierna Ziemniak: Czesc, czy kto wyjasni mi jak zrobic to zadanie? Dane sa funkcje f(x)=|x| oraz g(x)=1/(x−1). Wyznacz te argumemty x, dla ktorych funkcja f osiaga wartosci mniejsze niz funkcja g.

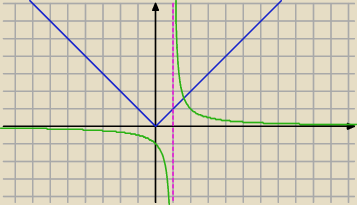
Jerzy: Potrafisz odczytać ?

piotr:

	1		1
( (x<0 ∧ −x <		) ∨ (x≥0 ∧ x <		) ) ∧ (x ≠ 1)
	x−1		x−1

5-latek:

	1
|x|<		dla x≠1
	x−1

	1		1
stad x<		i x>−
	x−1		x−1

nalezy rozwiazac te dwie nierownosci i wyznaczyc czesc wspolna rozwiazan

Jerzy: Cześć małolat

	1
Musi być dodatkowe założenie:		≥ 0 , bo prawa strona musi być nieujemna.
	x − 1

Ziemniak: Czesc wszystkim i dzieki za pomoc, ale nie jestem w stanie odczytac wartosci z wykresu Jerzy. Tzn nie jestem pewna ich prawidlowosci.

Jerzy: Odciętą puntu przecięcia trzeba obliczyć rozwiązując nierówność:

	1
x <		dla x > 1
	x − 1

piotr: ( ( x<0 ∧ −x<1/(x−1) ) ∨ ( x≥0 ∧ x<1/(x−1) ) ) ∧ (x≠0) ⇒ 1<x<1/2 (1 + √5)

Jerzy: Wystarczy tylko nierówność 9:53

5-latek: Witaj Jerzy

Ziemniak: Kurcze, przepraszam za ignoracje, ale nie rozumiem dlaczego mam rozwiazac rownanie x< 1/(x−1) x>1

5-latek: Nierownosc To wynika z wlasnosci wartosci bezwzglednej |x|<a ⇔ x<a i x>−a |x|≤a ⇔x≤a i x≥−a

5-latek: Druga (przydatna) jest taka |x|>a ⇔x>a lub x<−a |x|≥a ⇔x≥a lub x≤−a

Jerzy:

	1
Założenie:		≥ 0 ⇔ x > 1
	x − 1

Ziemniak: Ok, chyba wreszcie rozumiem, dziekuje za pomoc.