z zad:

1
	x2 – (m + 1)x + m2 + 3m + 2 = 0
2

ma dwa różne rozwiązania ujemne.

Jack: A noze tak tresc zadania?

zad: nie ma więcej

5-latek:

Eta: Parametr "m" musi spełniać układ warunków: 1/ Δ>0 i 2/ x₁+x₂<0 ⇒ −b/a<0 i 3/ x₁*x₂>0 ⇒c/a>0

zad: 1 Δ>0

	1
Δ=(m+1)2−4*1		*(m2+3m+2)
	2

m²+2m+1−2m²−6m−4>0 −m²−4m−3>0 (−4)²−4*(−1)*(−3)>0 4>0

	4−2
m1=		=−1
	−2

	4+2
m2=		=−3
	−2

m∊(−3,−1) 2 x₁+x₂<0

−b
	<0
2a

−(m+1)
	<0
1   2

2m+2<0 m<−1 3 x₁*x₂>0

c
	>0
a

m2+3m+2
	>0
1   2

2m²+6m+4>0 /2 m²+3m+2>0 Δ=3²−4*1*2 Δ=1

	−3−1
m1=		=−2
	2

	−3+1
m2=		=−1
	2

m∊(−∞,−2)∪(−1,+∞) m∊(−3,−2) Sprawdzi ktos

zad:

Eta: ok

zad: m∊(−3,−2) to tez

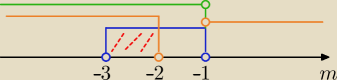Eta: 1/ Δ>0 ⇒m²+4m+3<0 ⇒ (m+3)(m+1)<0 ⇒ m∊(−3,−1) 2/ 2(m+1)<0 ⇒ m∊(−∞, −1) 3/ 2(m²+3m+2)>0 ⇒ (m+2)(m+1)>0 ⇒m∊(−∞,−2)U(−1,∞) wybierając część wspólną 1/ i 2/ i 3/ Odp: parametr m∊(−3,−2) ========= P.S ....... który zapis rozwiązania bardzie Ci się podoba ? chyba nie Twój "rozlazły" Na przyszłość podawaj rozwiązania w bardziej elegancki sposób (jak podałam Powodzenia

PW: A lepszego nicku niż "zad" nie mogłeś przyjąć?

Eta: Nick krótki: zad. a rozwiązanie ........................ rozlazłe

Eta: @PW "zad" jest bardzo ważną częścią ...... Pozdrawiam

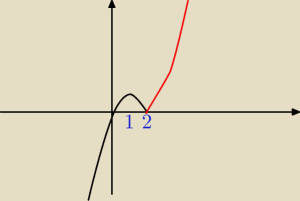zad: Naszkicuj wykres funkcji f(x) = –x · |x – 2| −określ maksymalne przedziały monotoniczności funkcji f −określ, dla jakiej wartości parametru m równanie f(x) = m ma trzy rozwiązania −podaj rozwiązanie nierówności f(x) > –1 1 f(x)=−x*|x−2| x≥2 f(x)=−x(x−2)=−x²+2x (czerwona) x<2 f(x)=−x(−x+2)=x²−2x(czarna) f(x)=−x²+2x f(0)=0 f(1)=−(1)²+2*1=1 f(2)=−(2)²+2*2=0 określ maksymalne przedziały monotoniczności funkcji f f(x)↗ (−∞,1)∪(2,+∞) f(x)↘ (1,2) określ, dla jakiej wartości parametru m równanie f(x) = m ma trzy rozwiązania nie wiem jak podaj rozwiązanie nierówności f(x) > –1 f(x)>−1 −x*|x−2|>−1 −x²+2x>−1 ∪ x²−2x<1 −x²+2x+1>0 x²−2x−1<0 Δ=2²−4*(−1)*1 (x−1)²<0 Δ=8 (x−1)(x+1)<0 √Δ=2√2 x₁<1 x₂<−1

	2−2√2
x1=		=√2−1 x∊(−1,1)
	−2

	2+2√2
x2=		=−√2−1
	−2

x∊(−√2−1,√2−1) x∊(−1,√2−1) dobre to

zad:

zad:

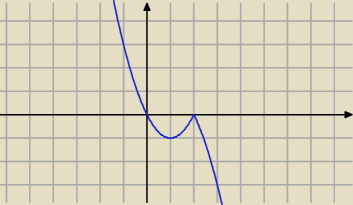
kochanus_niepospolitus: błędy już na samym początku: Pkt 1 dlaczego f(x) = x²−2x masz narysowaną jako (część) paraboli z ramionami skierowanymi do dołu A f(x) = −x²+2x ma ramiona skierowane do góry

kochanus_niepospolitus:

kochanus_niepospolitus:

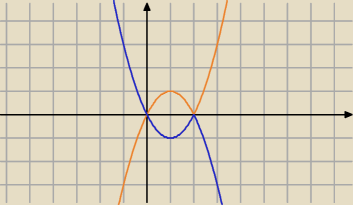
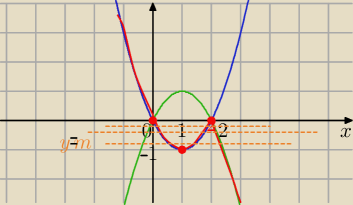Eta: 1/ dla x ≥2 część paraboli y= −x²+2x 2/ dla x<0 część paraboli y=x²−2x f(x) Wykres u Ciebie nie jest poprawny Maksymalne przedziały monotoniczności funkcji f(x) f(x) rośnie ⇔ x∊<1,2> f(x) maleje ⇔ x∊(−∞,1> U<2,∞) f(x)=m ma 3 rozwiązania ⇔ m∊(−1,0) f(x)>−1 ⇔ x∊(−∞,0)U (0,2> ( po czerwonej paraboli od lewej do miejsca zerowego 2 i bez x=0 oraz −x²+2x>−1 ⇒ x²−2x−1<0 dla x∊<2, 1+√2> Odp: f(x)>−1 ⇔ x∊(−∞,0) U (0, 1+√2> ==============================