płaszczyzna zespolona
zbłąkana_owieczka: narysuj na płaszczyźnie zespolonej zbiór:
| | 3 | |
{z∊C: |i(x − yi) −1 + i| ≤ √2 ⋀ |
| ≤ arg(3iz) ≤ 2π } |
| | 2 | |
Byłbym wdzięczny za wytłumaczenie tego, bo nie miałem jeszcze takich przykładów

1 lis 22:13
Adamm:
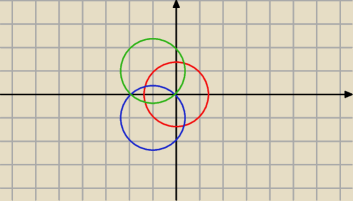
s(z) − sprzężenie z
|i*s(z)−1+i|≤
√2 ⇔ |i*s(z)+i
2+i|≤
√2 ⇔ |i|*|s(z)+1+i|≤
√2 ⇔
⇔ |s(z)−(−1−i)|≤
√2
skorzystaliśmy z własności |zw|=|z|*|w|
najpierw rysujemy obszar
|z|≤
√2 <− koło razem z brzegiem o promieniu
√2 (czerwony)
|z−(−1−i)|≤
√2 <− dokładnie to samo, tylko środek w −1−i (niebieski)
|s(z)−(−1−i)|≤
√2 <− odbijamy względem OX (zielony)
1 lis 22:24
Adamm: arg(3iz)=π/2+arg(z)
bo argumenty się dodaje, gdy mnoży się liczby zespolone
i dalej, normalnie
masz wyznaczyć liczby na płaszczyźnie o argumentach z jakiegoś tam przedziału
mam nadzieję że to potrafisz
1 lis 22:28
Adamm: arg(zw)=arg(z)+arg(w)
tak można zapisać tą własność
1 lis 22:29
zbłąkana_owieczka: dziękuję bardzo za pomoc
1 lis 22:59

 s(z) − sprzężenie z
|i*s(z)−1+i|≤√2 ⇔ |i*s(z)+i2+i|≤√2 ⇔ |i|*|s(z)+1+i|≤√2 ⇔
⇔ |s(z)−(−1−i)|≤√2
skorzystaliśmy z własności |zw|=|z|*|w|
najpierw rysujemy obszar
|z|≤√2 <− koło razem z brzegiem o promieniu √2 (czerwony)
|z−(−1−i)|≤√2 <− dokładnie to samo, tylko środek w −1−i (niebieski)
|s(z)−(−1−i)|≤√2 <− odbijamy względem OX (zielony)
s(z) − sprzężenie z
|i*s(z)−1+i|≤√2 ⇔ |i*s(z)+i2+i|≤√2 ⇔ |i|*|s(z)+1+i|≤√2 ⇔
⇔ |s(z)−(−1−i)|≤√2
skorzystaliśmy z własności |zw|=|z|*|w|
najpierw rysujemy obszar
|z|≤√2 <− koło razem z brzegiem o promieniu √2 (czerwony)
|z−(−1−i)|≤√2 <− dokładnie to samo, tylko środek w −1−i (niebieski)
|s(z)−(−1−i)|≤√2 <− odbijamy względem OX (zielony)