trójkąt mat17: Oblicz obwód i pole trójkąta wiedząc że promień okręgu wpisanego w ten trójkąt ma długość 4 a punkt styczności okręgu dzieli jeden z boków na odcinki długości 6 i 8

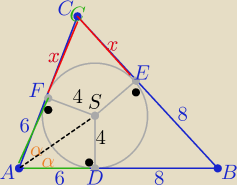
Eta: 1/ z tw. o odcinkach stycznych |AD|=|AE|=6 , |BD|=|BE|=8 i |EC|=|FC|=x , x>0 2/ P=rp p−− połowa obwodu , P−−pole Δ , p= 14 +x P(ABC)=4(14+x) 3/ w trójkącie ADS ( AS −− odcinek dwusiecznej ... dlaczego? ... |AS|= √36+16=2√13

	2		3
sinα=		i cosα=
	√13		√13

	12
sin(2α)=2sinα*cosα=
	13

	1		12
P(ABC)=		*|AB|*|AC|*sin(2α) = 7*(6+x)*
	2		13

to porównując pola : 4*13(14+x)= 7*12(6+x) ........................... x= 7 Obwód i pole ........ oblicz już samodzielnie 2/ sposób Można pole P(ABC) policzyć ze wzoru Herona i P=rp i też te pola porównać ....... i wyznaczyć x