Szkicowanie i własności funckji homograficznej Sylwia: Naszkicuj wykres funkcji homograficznej F. Omów jej własności, jeśli:

	x +1
a) F(x)=
	x − 1

	x−1
b) F(x) =
	x−4

	2x+4
c) F(x) =
	x+3

Sylwia: Trzeba wziąć pod uwagę takie własności jak: dziedzina, zbiór wartości, miejsce zerowe, monotoniczność, punkty przecięcia z osią OX i OY, środek symetrii i osie symetrii, wierzchołki, parzystość i równowartościowość funkcji

Janek191:

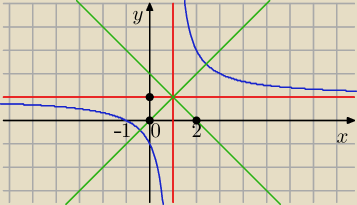
	x + 1		x − 1 + 2		2
a) f(x) =		=		=		+ 1
	x − 1		x − 1		x −1

D = ℛ \ { 1} ZW = ( −∞, 1) ∪ (1, +∞) Miejsce zerowe : x = − 1 Funkcja maleje w ( −∞, 1), ( 1 , +∞) Z osią OX: A = ( − 1, 0) Z osią OY: B = ( 0, −1) Środek symetrii P = ( 1, 1) Osie symetrii : y = x i y = − x + 2 itd.

Eta: Pięknie wykolorowane... Janek

Sylwia: Dziękuje bardzo a wierzchołki jak się oblicza?

Janek191: Przecięcie wykresu z prostą y = x

Janek191:

x + 1
	= x x ≠ 1
x −1

x + 1 = x² − x x² −2 x − 1 = 0 Δ = 4 − 4*1*(−1) = 4*2 √Δ = 2√2

	2 − 2√2
x =		= 1 − √2 lub x = 1 = √2
	2

i y = x więc C = ( 1 − √2, 1 − √2) D = ( 1 + √2, 1 + √2)

Sylwia: Naprawdę dziękuję! A jeszcze jedno pytanie jak zobaczyć czy ta funkcja jest parzysta, nieparzysta i różnowartościowa?

Janek191: Różnowartościowa, jeśli dla każdego x₁ . x₂ ; [ f(x₁} = f(x₂) ⇒ x₁ = x₂ ]

Janek191: Funkcja parzysta f(−x ) = f( x) Funkcja nieparzysta f(− x) = − f(x) Funkcja parzysta − jej wykres jest symetryczny względem osi OY Funkcja nieparzysta − jej wykres jest symetryczny względem O = ( 0, 0)

Sylwia: Dzięki wielkie! Już teraz rozumiem