MalWas: Dane mamy odcinki długości a i b oraz punkty A i B. Wyznacz miejsce geometryczne takich

	AP		a
punktów P płaszczyzny dla których		=		.
	PB		b

g: Dla uproszczenia przyjmijmy A=(1,0), B=(0,0), P=(x,y), a/b=r.

√(x−1)2+y2
	= r
√x2+y2

Po przekształceniach

	1		r
(x−		)2 + y2 = (		)2
	1−r2		1−r2

czyli to jest okrąg gdy r≠1, albo prosta gdy r=1.

MalWas: A jak to przedstawić geometrycznie

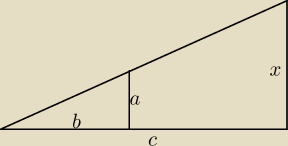g: Trzeba skonstruować dwa odcinki (załóżmy że a < b):

	1		b2
1) odległość środka okręgu od punktu B: S = AB*		= AB*
	1−r2		b2−a2

2) promień okręgu: R = S*r

	a
Rysunek pokazuje jak konstrukcyjnie wyznaczyć odcinek o długości x = c*		.
	b

Do wyznaczenia S i R trzeba tej konstrukcji użyć kilka razy

	b		b
S = (AB *		) *
	b−a		b+a

	a
R = S *
	b

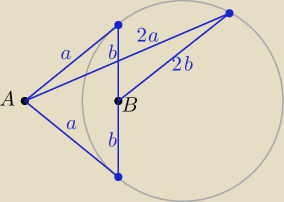g: Albo prościej Wg. rysunku: przy pomocy par (a,b), (2a,2b), lub jakiejkolwiek (k*a,k*b) wyznaczyć trzy punkty okręgu. Mając trzy punkty można już wyznaczyć środek okręgu i cały okrąg.

Mila: 1) a=b− symetralna AB

	a
2)		≠1 − Okrąg Apoloniusza.
	b

g może łatwiej pokazać dla przypadku r=2 i punktów jak podałeś 13:10. 3) Ja rozwiązałam dla A=(−1,0) i B=(1,0) i r=2