GEOMETRIA Kinia: TRÓJKĄT RÓWNORAMIENNY ABC, W KTORYM AC=BC ROZCIETO ODCINKIEM AD NA DWA TROJKATY ROWNORAMIENNE DAB I CAD TAK, ZE AB=DB I CD=AD. UDOWDONIJ ZE KAT ACB= 180STOPNI/7.

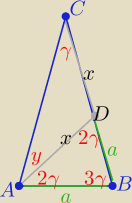
Eta: ΔADC równoramienny o kątach |∡DAC|=|∡DCA|=γ kąt ADB jest kątem zewnętrznym ΔADC zatem ma miarę 2γ ΔABD równoramienny to |∡BAD|=|∡BDA|=2γ i trójkąt ABC równoramienny to |∡BAC|=|∡ABC|=3γ zatem wΔABC :

	180o
7γ=180o ⇒ γ=
	7

c.n.w

Eta: @Kinia Czy oprócz wrzucania zadań ..... znasz takie słowo "dziękuję" ?

Kinia: @Eta − Tak, znam, i oczywiscie bardzo dziekuje Pani za pomoc, ale zadanie dodawalam o godzinie 00:43, później poszłam już spać i dzisiaj rano dopiero zobaczylam te odpowiedz do zadania. Jeszcze raz dziekuje.

Kinia: A dałoby sie tez to zadanie rozwiazac z podobienstwa trojkatow np. z cechy bkb?

5-latek: A mozesz nie krzyczec ? Zle sie czyta .

Kinia: Tak, przepraszam, tak jakos napisalam.

Jerzy: A gdzie tu widzisz trójkąty podobne ?

Kinia: Nie wiem. Tak po prostu zapytałam.