W oparciu o twierdzenie o sumie miar katow w trojkacie uzasadnij, że suma miar k Kinia: W oparciu o twierdzenie o sumie miar katow w trojkacie uzasadnij, że suma miar katow dowolnego n−kata wypuklego wynosi (n−2)π.

Kinia: Na przeciwprostokątnej AB trojkata prostokatnego ABC wybrano punkty D i E w taki sposob, by lACl=lAEl oraz lBCl=lBDl. Udowodnij, że lkąt DCEl= π/4.

5-latek: Bokow musi byc wiecej niz 3 w takim wielokacie Wzor ten jest dla katow wewnwtrzych wielokata Chca obliczyc sume tych katow dzielimy wielokat wypukly na trojkaty w ten sposob z ez jednego wierzcholka wielokata wykreslamy wszystkie mozliwe przekatne zwroc uwage na to ze ilosc otrzymanych trojkatow jest zawszse o 2 mniejsza niz ilosc bokow wielokata czyli ilosc trjjkatow to (n−2) suma katow w trojkacie to 180^o wiec suma k atow wewnetrznych wielokata wypuklego to (n−2)*180^o Zrob sobie pare rysunkkow (np 5−kata , czy innego wielkokata

Kinia: dziekuje : )

Jerzy: małolat ... niestety to co napisałeś niczego nie uzasadnia

5-latek: Jerzy Taki dowod mam w swojej ksiazce . Ewentualnie potem zobacze do Krygowskiej albo Janowskiego .

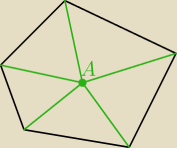
Jerzy: n kąt dzielimy na n trójkątów suma katów przy wierzchołkach A = 360^o suma wszystkich katów wielokąta, to suma wszystkich katów przy podstawach trójkątów czyli: SUMA KĄTÓW WIELOKĄTA = n*180^o − 360^o = 180^o*(n − 2) (od sumy wszystkich katów wszystkich trójkątów odejmujemy sumę kątów przy wierzchołkach A)

5-latek: OK Najtrudniejszse sa dowody oczywiste