Okrąg opisany na trapezie darek: Oblicz obwód trapezu wpisanego w okrąg o promieniu 3 cm wiedząc, że dłuższa podstawa trapezu jest średnicą tego okręgu oraz przekątna trapezu ma długość 2√7

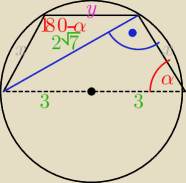
yht: Trapez równoramienny (kąt między przekątną a ramieniem będzie prosty bo to kąt oparty na średnicy okręgu) x²+(2√7)² = 6² x² + 28 = 36 x² = 8 x = 2√2

	2√2
cosα =
	6

	√2
cosα =
	3

	√2
cos(180o−α) = −cosα = −
	3

z tw. cosinusów w górnym trójkącie (2√7)² = x²+y²−2xy*cos(180⁰−α)

	√2
28 = 8+y2−4√2*(−		)*y
	3

	8
28 = 8+y2+		y
	3

	8
y2+		y−20 = 0
	3

3y²+8y−60 = 0 Δ = 64−4*3*(−60) = 64+720=784 → √Δ = 28

	−8−28
y1 =		< 0 nie spełnia warunków zadania
	6

	−8+28		20		10
y2 =		=		=
	6		6		3

	10		1
Ob = 6 + 4√2 +		= 9		+4√2
	3		3

darek: Nie spodziewałem się użycia twierdzenia cosinusów, bo dopiero będzie za 3 tematy. Dzięki.

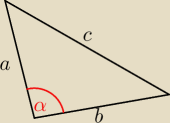yht: twierdzenie cosinusów, to taki podrasowany Pitagoras c²=a²+b²−2ab*cosα gdy α=90⁰ (szczególny przypadek) to c²=a²+b²−2ab*cos90⁰ c²=a²+b²−2ab*0 c²=a²+b²

darek: Podrasowany Pitagoras. Podoba mi się to stwierdzenie, dzięki.

Eta:

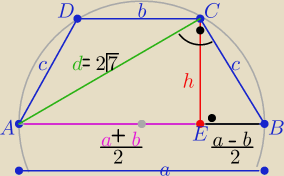
	6+b		6−b
a=|AB|=2R=6 i |AE|=		, |EB|=
	2		2

z tw. Pitagorasa c=√36−28=√8=2√2

	d*c		2√14
h=		=
	a		3

W ΔABC : h²=|AE|*|EB|

	56		(6+b)( 6−b)		224		100		10
to		=		⇒ 36−b2=		⇒ b2=		⇒ b=
	9		4		9		9		3

	1
Obwód trapezu L=2c+a+b= 4√2+9
	3

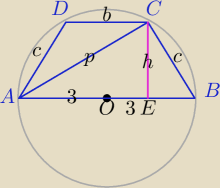Mila: II sposób 1) c²=6²−(2√7)²=8 c=2√2 2)

	1
PΔABC=		*c*p
	2

P_ΔABC=2√14

	1
2√14=		*6*h
	2

	2√14
h=
	3

3) |AE|²=p²−h²

	14
|AE|=
	3

	a+b
|AE|=
	2

	28
a+b=
	3

	28
Obw=		+4√2
	3

==============

darek: Dziękuje ślicznie wszystkim. Teraz to na pewno zrozumiem.