Nierówność z wartością bezwzględna
Kalirr: Witam. Pomożecie?
Rozwiąż nierówność |x−1|−3x≥|x+2|
W pierwszym przedziale wychodzi mi x≤1
W drugim x≤−1/5
W trzecim x≤−1
Co się sumuje do x∊(−∞;−1> a w książce jest odpowiedź x∊(−∞;−1/5).
Gdzie mam błąd?
29 paź 19:22
5-latek: Nie wiem Przedstaw obliczenia
29 paź 19:23
czujek22: Dla przedziału (−∞;−2>:
−x+1−3x ≥ −x−2
−3x ≥ −3
x ≤ 1
Dla przedziału (−2;1>:
−x+1−3x ≥ x+2
−x−x+1−2−3x ≥ 0
−5x ≥ 1
x ≤ −1/5
Dla przedziału (1;+∞):
x−1−3x ≥ x+2
x−x−3x ≥ 3
−3x ≥ 3
x ≤ −1
29 paź 19:30
czujek22:
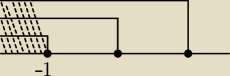
29 paź 19:33
Mila:
|x−1|−3x≥|x+2|
1)x<−2
−(x−1)−3x≥−(x+2)
−x+1−3x≥−x−2
−3x≥−3
x≤1 i x<−2⇔
x<−2
lub
2) x∊<−2,1)
−(x−1)−3x≥(x+2)
−x+1−3x≥x+2
| | 1 | |
−5x≥1 ⇔x≤− |
| i x∊<−2,1)⇔ |
| | 5 | |
lub
3) x>1
x−1−3x≥x+2
−3x≥3
x≤−1 i x>1 brak rozwiązania
odp.
29 paź 19:34
czujek22: Dzięki za wyjaśnienie, nie wiedziałem, że trzeba brać potem pod uwagę przedziały na których się
sprawdza.
Ps. To ja założyłem temat tylko pod innym nickiem
29 paź 19:42
Mila:

29 paź 22:17

