Twierdzenie sinusów Paweł: Rozwiąż trójkąt o danych bokach i kącie wiedząc, że miary pozostałych kątów są nie większe, niż 90*. a) a=4, b=8, α =30

kochanus_niepospolitus: Rozwiąż trójkąt Co to w ogóle ma oznaczać?

Eta: Rozwiązać trójkąt to znaczy: podać długości boków i miary kątów tego trójkąta

Paweł: Dokładnie.

Paweł: Ktoś pomoże?

kochanus_niepospolitus: mam rozumieć, że kąt jest pomiędzy a i b

Paweł: Kąt α jest naprzeciwko boku a. Jeżeli nie jest napisane inaczej to przyjmuje się że α, β, γ leżą naprzeciwko boków a, b, c.

Eta:

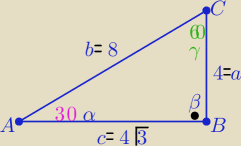
	4		8
1/ z tw. sinusów		=		⇒ sinβ=1 ⇒ β=90o
	sin30o		sinβ

ten trójkąt jest prostokątny zatem γ= 60^o i c= √8⁸²−4²=√48=4√3

kochanus_niepospolitus: no to z tw. cosinusów: a² = c² + b² − 2bc*cos30^o

	√3
16 = c2 + 64 − 16c*
	2

wyznacz 'c' mając trzy boki z tw. cosinusów wyznaczasz drugi kąt. Mając dwa kąty, z sumy kątów wyznaczasz trzeci kąt.

Paweł: A to takie proste. Dzięki Eta. ____ Twierdzenie cosinusów będę przerabiał później, ale dzięki.

Eta: