Wyznacz równanie symetralnej odcinka AB, jeżeli A=(-4,-6), B=(2,-4). lotnik: Wyznacz równanie symetralnej odcinka AB, jeżeli A=(−4,−6), B=(2,−4).

PW: Punkt P = (x,y) leżący na symetralnej jest jednakowo oddalony od końców odcinka. Zapisz to w postaci równania.

Janek191:

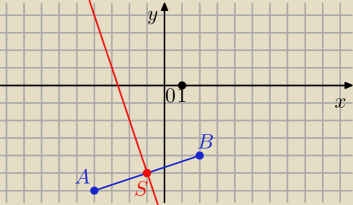
	− 4 − (−6		1
a =		=
	2 − (−4)		3

a₁ = − 3 S = ( −1, − 5) więc y = − 3 x + b − 5 = − 1*(−3) + b ⇒ b = − 8 Odp. y = − 3 x − 8 ============

PW: Janek191 rozwiązał to inną metodą niż proponowałem − poprowadził przez środek odcinka prostopadłą. Dla urozmaicenia metod zróbmy "po mojemu" (porównajmy kwartaty odległości od końców odcinka): (x−(−4))² + (y−(−6))² = (x−2)² + (y−(−4))² (x+4)² + (y+6)² = (x−2)² + (y+4)² x²+8x+16 + y²+12y+36 = x²−4x+4+y²+8y+16 8x+12y+32=−4x+8y 12x+4y+32 = 0 3x+y+8 = 0, i jest to ta sama prosta, którą wyznaczył Janek191, inaczej być nie mogło.