Zaznacz następujące zbiory w przestrzeni zespolonej Paweł: Witam! Czy mógłby mi ktoś rozwiązać te zadania potrzebuje tych podpunktów jeszcze na dzisiejsze zajęcia 𝑎) 𝑆 = {𝑧∈𝐶: 1 ≤|𝑧 + 3 − 2𝑖| ≤ 4 }, b) 𝑆 = {𝑧∈𝐶: |# −2 +2𝑖| >√2+3i }, (# to sprzężona) c) 𝑆= {z∊C: −^3π₄ ≤ arg (z−2+i) ≤ ^π₂,

Jerzy: a) 1 ≤ | z − ( −3 + 2i)| ≤ 4 , to pierscień o środku w punkcie z₀ = (−3 + 2i) i promieniach r₁ = 1 , r₂ = 4 Potrafisz to narysować ?

Adamm: c) rysujesz obszar −3pi/4≤arg(z)≤pi/2, i przesuwasz o wektor 2−i (lub [2; −1])

Paweł: Właśnie problem polega u mnie głównie na narysowaniu tego

PW: a) 1²≤|z−(−3+2i)|≤2² Liczba z jest odległa od (−3+2i) o co najmniej 1 i co najwyżej o 4. Oznacza to, że liczba z leży w pierścieniu kołowym wyznaczonym przez koła o środku (−3,2) i promieniach 1 oraz 2.

Jerzy: Witaj PW , popraw promień większego okręgu.

PW: Spóźniłem się i sknociłem. Nie czytać.

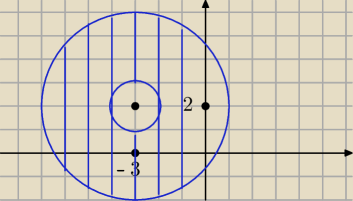
Jerzy: To masz do a)