prosze o wytłumaczenie Dobra: Wytłumaczy mi ktoś ten przykład? https://zapodaj.net/428f622463309.png.html

Jerzy:

	cosx		sinx		cosx + 1
⇔		+		< 2 ⇔		< 2
	sinx		1 + cosx		sinx(1 + cosx)

kochanus_niepospolitus: więc zaczniemy od podstaw:

	cosx
ctgx =
	sinx

sinx = 0 ... dla jakiego x stąd x=0 ; x=π i x=2π wypadają z badanego przedziału dla tejże nierówności. 1) niech x∊(0,π);

cosx		sinx
	< 2 −		//*sinx (zauważ, że: sinx >0)
sinx		1+cosx

	sin2x
cosx < 2sinx −		(stosujemy jedynkę trygonometryczną w liczniku)
	1+cosx

	1 − cos2x
cosx < 2sinx −		(kłaniają się wzory skróconego mnożenia)
	1+cosx

	(1 − cosx)(1+cosx)
cosx < 2sinx −
	1+cosx

cosx < 2sinx − 1 + cosx 0 < 2sinx − 1 1 < 2sinx

	1
sinx >
	2

x ∊ (... , ...) 2) niech niech x∊(π, 2π)

cosx		sinx
	< 2 −		//*sinx (zauważ, że: sinx <0)
sinx		1+cosx

	sin2x
cosx > 2sinx −		(stosujemy jedynkę trygonometryczną w liczniku)
	1+cosx

itd.

Jerzy: Aleś się nakombinował

	1
10:10 ... delej ⇔		< 2
	sinx

Dobra: Nie rozumiem tych przedziałów, dlaczego mamy rozpatrywac te punkty 1 i 2 ?

Jerzy:

	1
Masz:		< 2
	sinx

Dla sinx > 0

	1
..... ⇔ 1 < 2sinx ⇔ sinx >
	2

Dla: sinx < 0

	1
....... ⇔ 1 > 2sinx ⇔ sinx <
	2

Jerzy: 1) sinx > 0 ⇒ x ∊ (0;π) 2) sinx < 0 ⇒ x ∊ (π,2π)

Jerzy:

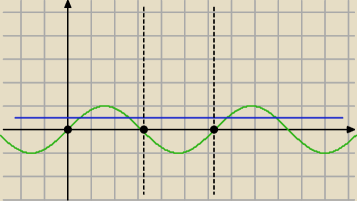
	1
Niebieska: y =
	2

Dobra: Dziękuje bardzo już rozumiem

Dobra: Mam jeszcze jeden problem https://scontent-waw1-1.xx.fbcdn.net/v/t34.0-12/22835537_888630547972843_1433340414_n.png?oh=e9751f0cf7c52b45822c1c38bf95d9a3&oe=59F48EEC rozwiazałam równanie, ale nie umiem wyznaczyc przedziału brzmi glupio ... ale zbłądziłam tutaj

Jerzy:

	1
Patrz na swój rysunek. Odpadną tylko kąty pod kreską i te , dla których sinx =		lub 1
	2

Dobra: Nie potrafie tego wyznaczyc .. Będzie xe( 0; π/2 ) ? (π; 2π) ?

Jerzy: Ustal jakie kąty wyznaczają te dwie czarne kropki na Twoim rysunku.

Dobra: 220 stopni, a drugi 330 stopni

Dobra: 210 pierwszy*

Jerzy: Teraz te, dla których sinx = 1

Dobra: 90 stopni

Dobra: a dalej?

Jerzy:

	π		π		7		11
Teraz patrz vna rysunek: x ∊ [0;		) U (		;		π) U (		π;2π]
	2		2		6		6

Dobra: Now I know, thx

Jerzy: Great !