Nierówności Maciek: Rozwiąż nierówność. Proszę o pomoc:

	3
| log2/3 (2 −		) | > 1
	x+2

5-latek:

	3
Zalozenie 2−		>0
	x+2

potem z wlasnosci wartosci bezwzglednej |a|>k ⇔a>k lub a< −k

Maciek: Dziedzina: x ∊ (−∞; −2) ∪ (1/2; +∞) Przedział dla a > k: x > −1 Wychodzi mi x ∊ (−∞; −2) ∪ (1/4; +∞), czyli x ∊ (1/4; +∞) Przedział dla a < k: x < 1 Wychodzi mi x ∊ (−2; −7/8), czyli x ∊ (−2; −7/8) Jest to całkowicie sprzeczne z odpowiedziami, które wynoszą x ∊ (−∞; −2) ∪ (−1/2; 1/4) ∪ (4; +∞)

Jerzy: Pokaż rachunki.

Jerzy: Przecież np. x = 0 należy do dziedziny.

Maciek: Dziedzina:

	3
2 −		> 0
	x+2

2x + 4 − 3
	> 0
x+2

(2x + 1)(x + 2) > 0 x ∊ (−∞; −2) ∪ (−1/2; +∞) |a| > k

	2x + 1
1) a > k <=> log2/3 (		) > 0
	x + 2

	2x + 1
log2/3 (		) > log2/3 1
	x + 2

2x + 1
	> 1
x + 2

2x + 1 > x + 2 x > −1

	2x + 1
log2/3 (		) > log2/3 2/3
	x + 2

2x + 1
	> 2/3 | * 3
x + 2

6x + 3
	> 2
x + 2

6x + 3 − 2x − 4
	> 0
x + 2

(4x − 1)(x + 2) > 0

	2x + 1
2) a < k <=> log2/3 (		) < 0
	x + 2

	2x + 1
log2/3 (		) < log2/3 1
	x + 2

2x + 1
	< 1
x + 2

2x + 1 < x + 2 x < −1

	2x + 1
−log2/3 (		) > log2/3 2/3
	x + 2

−2x − 1
	> 2/3 | * 3
x + 2

−6x − 3
	> 2
x + 2

−6x − 3 − 2x − 4
	> 0
x + 2

(−8x − 7)(x + 2) > 0

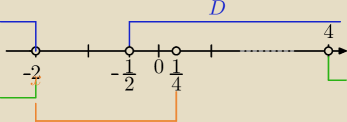Mila: 1) D:

	3
2−		>0 i x≠−2
	x+2

2*(x+2)−3
	>0
x+2

2x+1
	>0⇔(2x+1)*(x+2)>0 i x≠−2
x+2

	1
x<−2 lub x>−
	2

2)

	3		3
log2/3(2−		)<−1 lub log2/3(2−		)>1
	x+2		x+2

	3		2
log2/3(2−		)<log2/3(		)−1
	x+2		3

	3		2
lub log2/3(2−		)>log{2/3)(		)1⇔ funkcje malejące, odwracamy nierówności
	x+2		3

	3		3		3		2
(2−		)>		lub (2−		)<		⇔
	x+2		2		x+2		3

x−4		4x−1
	>0 lub		<0
x+2		x+2

	1
[x<−2 lub x >4] lub [x∊(−2,		] i x∊D
	4

	1		1
x∊(−∞,−2) ∪(−		,		)∪(4,∞)
	2		4

Maciek: Wielkiej dzięki i dobrej nocy. Jeśli mogę mieć jeszcze pytanie − funkcja jest malejąca w przypadku funkcji wykładniczej, gdy podstawa wynosi a ∊ (0; 1). W przypadku funkcji logarytmicznej jest tak samo?

Mila: Tak. Dobranoc