Trójkat Pomocy!: Na kole o promieniu R opisano trójkąt prostokątny o najmniejszym polu. Znaleźć długości boków tego trójkąta.

kochanus_niepospolitus: O najmniejszym polu? To będzie trójkąt prostokątny równoramienny. Więc trójkąt będzie miał boki długości: x, x, x√2

	√2		2R		2R(2+√2
R +		x = x −> x =		=		= (2+√2)R
	2		2−√2		4−2

więc mamy boki: (2+√2)R (2+√2)R (2√2+2)R

Maciek:

	abc		abc
R=		⇒ P=
	4P		4R

wiemy, że c²=a²+b² i a=2R

	b√4R2+b2
P=
	2

P będzie najmniejsze kiedy b=0 Długości boków: a=2R, b=0, c=2R

kochanus_niepospolitus: Maciek ... a o kiedy trójkąt może mieć bok = 0

kochanus_niepospolitus: i skąd założenie, że a = 2R Skoro to na okręgu OPISANO trójkąt (a nie wpisano w okrąg)

Eta: Jak nie istnieje !

kochanus_niepospolitus: zresztą nawet jakby to był wpisany, to wtedy c=2R

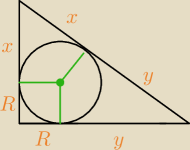
kochanus_niepospolitus: zał. x,y > R

	Ry
(x+y)2 = (R+x)2 + (R+y)2 ⇔ 2xy = 2R(x+y) ⇔ x(y−R) = Ry ⇔ x =
	y−R

	(R+x)(R+y)		R2 + R(x+y) + xy		R2 + R(x+y) + R(x+y)
P =		=		=		=
	2		2		2

	R2 + 2R(x+y)
=		... podstawiasz ... pochodna po 'x' i jedziesz z koksem, aby wyszło,
	2

że ekstremum będzie dla x=y

Korol: Kochanus, brakuje ci 2R² w twierdzeniu pitagorasa