Parametr Ajtek: Witam, problem do jasnej anielki . Kwadratowa z parametrem. (x−3m)(x−m−3)<0 dla jakiej wartości parametru m nierówność jest prawdziwa dla każdej liczby rzeczywistej należącej do przedziału <1;3> Jak to dziabnąć? Postawiłem warunki: Δ>0 f(1)≥0 f(3)≥0 I bzdury wychodzą wg odpowiedzi w zbiorze . Help...

Adamm: np. tak 1. 3m=m+3 m=3/2 (x−3/2)²<0 nie zachodzi dla żadnego x 2. 3m<m+3 m<3/2 x∊(3m; m+3) 3m<1 m+3>3 0<m<1/3 3. 3m>m+3 m>3/2 x∊(m+3; 3m) m+3<1 3m>3 sprzeczność czyli dla m∊(0;1/3)

Adamm: zbyt schematycznie myślisz (moja opinia)

Ajtek: Podziękował . Na to nie wpadłem, tzn. nie pamiętałem tego sposobu .

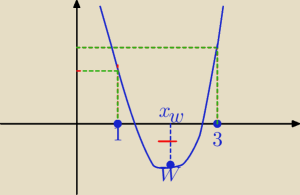
Eta: f(1)>0 i f(3)>0 (1−3m)(−m−2)>0 ⇒ m∊(−2,1/3) i (3−3m)(−m)>0 ⇒ m∊(0,1) Odp: m∊(0,1/3) ==============

Ajtek: Dzięki Eta, ten sposób coś mi świtał, ale tez nie pamiętałem do końca .