Prosze o pomoc. Magda: Oblicz sin kąta ACB Znajdź takie D aby ABCD był rownoleglobokiem. https://zapodaj.net/images/95853b9bf053d.jpg Pomoże ktoś?

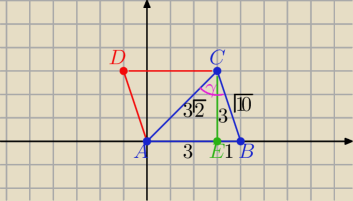
Eta: |AB|=4 , |CE|=3

	1
P(ABC) =		*4*3=6
	2

|AC|=3√2, |BC|=√10

	1		1		2√5
P(ABC)=		*|AC|*|BC|*sinγ ⇒		*3√2*√10*sinγ=6 ⇒ sinγ=
	2		2		5

aby czworokąt ABCD był równoległobokiem to → → AB= DC ⇒ to punkt D powstaje przez przesunięcie równoległe punktu C o wektor [−4,0] D( 3 −4,3−0) ⇒ D (−1,3)

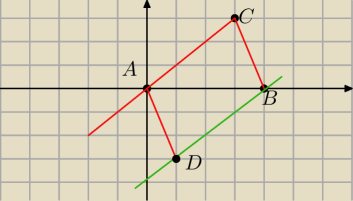5-latek: Rownolegobok mm adwie pary bokow rownoleglych 1) Rownanie prostej rownoleglej do CB i przechodzacej przez punkt A 2) rownanie prostej rownoleglej do AC i przechodzacej przez B 3) wyznaczasz punkt wspolny D W punkcie 1 wyznaczylas rownanie prostej CB a punkcie 2 rownanie prostej AC Jesli masz je w postaci ogolnej to tak zostaw Jesli w postaci kierunkowwej to zamien na ogolna Niech prosta CB ma posatc A_x+B_y+c=0 Prosta AC ma posatc A₁x+B₁y+c₁=0 Sinus kata miedzy tymi prostymi

	|A*B1−A1*B|
sinφ=
	√a2+B2*√A12+B12

Punkt D mozesz tez znalezc z wlasnosci dzielenia sie przekatnych na polowy Kat miedzy prostymi np tez zz iloczynu skalarnego (ale to bedzie cosinus i wtedy z jedynki tryg wyznaczysz sinus MOzan tez kat wyznaczyc z te cosi usow . Masz duzo mozliwosci wiec milej zabawy

5-latek: Drugi punkt D wyznaczyla Eta Dobry wieczor

Eta: Równoległobok miał być ABCD ( kolejno a nie ACBD

5-latek: No to zawalilem