punkty przecięcia
mp: Ile punktów przecięcia mają wykresy funkcji:
f(x) = 5x
g(x) = 1,6x+1
Jeden na pewno − (0,1), a gdzie jest drugi?
24 paź 20:00
Janek191:
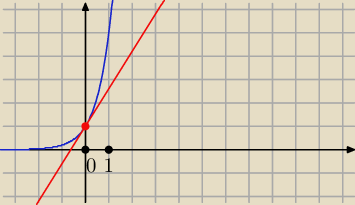
24 paź 20:27
5-latek: Drugi ktoś zajumał

24 paź 20:29
mp: Z wykresu nie wygląda, żeby były dwa... a są na pewno. Jak to pokazać?
24 paź 21:17
24 paź 21:26
kochanus_niepospolitus:
h(x) = f(x) − g(x) = 5
x − 8x/5 − 1
h'(x) = 5
xln5 − 8/5
| | 8 | |
h'(x) = 0 ⇔ 5x = |
| ⇒ x < 0 ale x≈0 |
| | 5ln5 | |
tak więc funkcja h(x) posiada jedno ekstremum ... skoro jednym z miejsc zerowych h(x) jest x=0
oraz lim
x−>−∞ h(x) = +
∞
stąd wniosek:
musi na pewno być jeszcze jeden x (i to x<0) dla którego h(x) = 0
Jako, że funkcja h(x) jest ciągła i posiada tylko jedno ekstremum, to mamy dokładnie dwa punkty
dla których f(x) = g(x) (czyli h(x) = 0)
24 paź 21:41
mp: O dzięki jeden dowód już jest

A da się to wywnioskować tylko z tego, że pochodne obu funkcji w punkcie przecięcia nie są
równe?
f'(x) = x
5ln5
f'(0) = ln5 ≠ 1,6
24 paź 22:08
mp: * oczywiście chodziło o f'(x)=5xlin5
24 paź 22:09
piotr: rozwiązaniem jest granica następującego ciągu rekurencyjnego
x
0 = −1
| | 5xn−1,6xn−1 | |
xn+1 = xn − |
| |
| | 5xnln(5)−1,6 | |
x ≈ −0,00731577457817074
24 paź 22:18
piotr: A da się to wywnioskować tylko z tego, że pochodne obu funkcji w punkcie przecięcia nie są
równe?
Tak, bo jeśli byłyby równe to byłaby styczna, a więc jeden punt wspólny.
24 paź 22:21
Adamm: ja mam taką sugestię, jeśli chodzi jedynie o wykazanie że ten pierwiastek istnieje
wyznacz styczną do 5x o nachyleniu 1,6, potem sprawdź czy jej współczynnik
wolny jest <1
jeśli tak, to mamy dwa pierwiastki
24 paź 22:22
mp: Piotr − niekoniecznie − styczna w jednym punkcie może się przecinać z funkcją gdzie indziej.
Adamm − wydaje się ok, ale chyba wystarczy, że współczynnik wolny ≠1.
24 paź 22:42
Adamm: faktycznie
nie może być >1 bo wiemy że jeden punkt wspólny już jest
w takim razie zadanie jest jeszcze łatwiejsze

24 paź 22:46
piotr: ale funkcja 5x jest ściśle monotoniczna w R, a więc styczna z jej wykresem nie może mieć
innych punktów wspólnych
25 paź 07:33
kochanus_niepospolitus:
mp jak tak bardzo chcesz to można w taki sposób:
| | 8 | | 8 | |
h'(0) = 50ln5 − |
| = ln5 − |
| > 0 |
| | 5 | | 5 | |
skoro h(0) = 0 i h'(0) > 0 to funkcja h(x) jest rosnąca w otoczeniu punktu x
0 = 0
jako, że:
lim
x−>+∞ h(x) = +
∞
lim
x−>−∞ h(x) = +
∞
funkcja h(x) jest funkcją ciągłą dla x∊R
∃
c≠0 h(c) = 0
Ale UWAGA

To pokazuje tylko, że punktów przecięcia jest co najmniej dwa. Tylko ten sposób
który podałem pokazuje, że jest to dokładnie dwa.
Piotr −−− zgoda, ale pytanie brzmi o ilość przecięć. Wyliczenie kolejnego przecięcia nie jest
równoznaczne z pokazaniem, że przecięć nie będzie więcej jak 2
25 paź 08:30


 A da się to wywnioskować tylko z tego, że pochodne obu funkcji w punkcie przecięcia nie są
równe?
f'(x) = x5ln5
f'(0) = ln5 ≠ 1,6
A da się to wywnioskować tylko z tego, że pochodne obu funkcji w punkcie przecięcia nie są
równe?
f'(x) = x5ln5
f'(0) = ln5 ≠ 1,6

 To pokazuje tylko, że punktów przecięcia jest co najmniej dwa. Tylko ten sposób
który podałem pokazuje, że jest to dokładnie dwa.
Piotr −−− zgoda, ale pytanie brzmi o ilość przecięć. Wyliczenie kolejnego przecięcia nie jest
równoznaczne z pokazaniem, że przecięć nie będzie więcej jak 2
To pokazuje tylko, że punktów przecięcia jest co najmniej dwa. Tylko ten sposób
który podałem pokazuje, że jest to dokładnie dwa.
Piotr −−− zgoda, ale pytanie brzmi o ilość przecięć. Wyliczenie kolejnego przecięcia nie jest
równoznaczne z pokazaniem, że przecięć nie będzie więcej jak 2