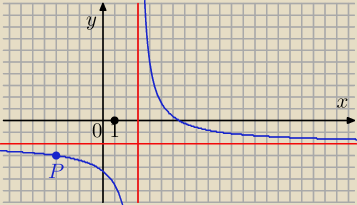
hiperbola wiktoria: Mam wykres hiberboli, asymptoty: pionowa x=3 y= −2 i punkt należący do wykresu (−4,−3)

	ax+b
polecenie. Funkcja przedstawiona na rysunku jest określona wzorem y=		znajdź
	x+c

wartości współczynników a,b,c. Niby podstawiam, ale wychodzi za dużo niewiadomych. Jak to zrobić?

kochanus_niepospolitus: to pokaż jak podstawiasz

Jerzy: To podstawiaj faktycznie, a nie na niby. Dwa równania są oczywiste, trzecie uzyskasz przekształcając do postaci kanonicznej.

kochanus_niepospolitus: 1) skoro x=3 jest asymptotą, to: 3+c = 0 ⇔ c = −3

	ax+b
więc już wiemy, że y =
	x − 3

2) skoro y = −2 jest asymptotą, to:

a
	= −2 −> a = −2
1

	−2x + b
więc już wiemy, że y =
	x−3

3) skoro punkt (−4, −3) należy do tej funkcji, to: .... już sama dokończ

wiktoria: rozbiłam na dwa ułamki

	a(x+c)		b−ac		b−ac
y=		+		= a+
	x+c		x+c		x+c

i wedlug mnie zle mysle bo teraz a to niby igrekowa asymptota czyli −3, a w mianowniku iksowa ze zmienionym znakiem będzie równa 3, idąc tym tokiem myślenia dalej wychodzi głupota

	b−ac
y= −3+		teraz za x i y wstawiam współrzedne punktu należacego do wykresu
	3+c

	b−ac
−3=−3+		i to jest głupota myślałam wziąć drugi punkt z symetrii należacy do drugiej
	3+c

hiperboli ale i tak mam wciąż brak danych.

wiktoria: chyba że za "a" do mianownika wstawić −3

Janek191:

	a x + b
y =
	x − 3

oraz

	− 4 a + b
−3 =		⇒ 21 = − 4 a + b ⇒ b = 4 a + 21
	− 7

więc

	a x + 4 a + 21
y =
	x − 3

	(x − 3) *a + 7 a + 21		7 a + 21
y =		= a +
	x −3		x − 3

więc a = − 2 i b = 13

	− 2 x + 13
y =
	x − 3

Jerzy: 1) Pierwsza linijka u Ciebie ... i widzisz,że a = −2 2) 3 + c = 0 ⇔ c = −3 ( patrz 10:50) 3) f(−4) = −3 i po zadaniu.

wiktoria: kochanus_niepospolitus: kurcze takie oczywiste a ja jakos idiotycznie krązyłam, asymptoty, asymptoty,asymptoty,asymptoty,asymptoty, do zera !

wiktoria: wiem, dziękuję wam <buziaki>