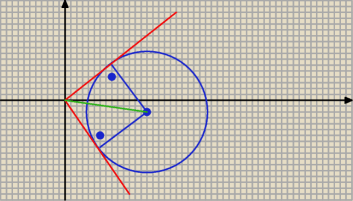
udowadnianie, planimetria wer: do okręgu x²−28x+y²+4y+100=0 poprowadzono styczne przechodzące przez poczatek ukladu wspolrzednych. Udowodnij że te proste sa prostopadle

kochanus_niepospolitus: zacznij od wyznaczenia środka tego okręgu i promienia

: to nie planimetria tylko geometria analityczna wystarczy podstawić do wzorów: https://matematykaszkolna.pl/strona/3423.html i rozwiązać układ r−ń

Janek191: x² − 28 x + y² + 4 y + 100 = 0 ( x − 14)² − 196 + ( y + 2)² − 4 + 100 = 0 ( x −14)² + ( y + 2)² = 10² d² = 14² + 2² = 200 = 2*100 więc d = 10 √2 Czworokąt jest kwadratem.

iteRacj@: otrzymasz współrzędne środka (14, −2) równania stycznych 4x + 3y = 0 , −3x + 4y = 0 masz tylko wykazać ich prostopadłość

the foxi: x²−28x+y²+4y+100=0 x²−28x+y²+4y+200=100 x²−28x+196+y²+4y+4=100 (x−14)²+(y+2)²=100 (x−14)²+(y+2)²=100² <−−− równanie okręgu Zauważ też, że styczne przechodzą przez punkt (0;0). Dalej chyba sobie poradzisz. (:

iteRacj@: the foxi jedno zero wskoczyło równanie okręgu (x−14)²+(y+2)²=10²

wer: równanie stycznej liczę ze wzoru odleglosc=10 punktu (14,−2) od prostej Ax+By+C=0?

5-latek: Ale wspolrzedne punktow stycznosci mozna tez otrzymac jesli sie zna konstrukcje stycznej do okreg jesli punkt lezy poza okregiem (wlasnie z planimetrii Poza tym rysunek nalezy zrobic .

iteRacj@: wer Ax+By=0 , wykorzystaj że C = 0

wer: iteRacj@: mógłbyś pokazać jak rozpisałeś jedno równanie stycznej np 4x + 3y = 0? coś mi nie wychodzi chyba tak jak powinno

5-latek: Skoro styczna ma przechodzic przez punkt (0,0) to jesj rownanie bedzie takie y=m(x−x₀)+y₀ y= m(x−0)+0 y=mx Wspolczynnik m znajdziesz np tak Wiec uklad rownan {y=mx {(x−14)²+(y+2)²=100 musi miec jedno rozwiazanie

iteRacj@: równanie prostej stycznej do okręgu, przechodzącej prze pkt (0,0) Ax + By = 0 współrzędne środka okręgu (14, −2) czyli x_o =14, y_o = −2 długość promienia 10

	|A*14 + B*(−2)|
10 =
	√A2 + B2

	|A*7 − B|
5 =		/obie strony są dodatnie, podnoszę do kwadratu
	√A2 + B2

	(A*7 − B)2
25 =
	A2 + B2

	4		−3
stąd A =		B lub A =		B
	3		4

iteRacj@: równania prostych

4
	x + y = 0 → 4x + 3y = 0
3

−3
	x + y = 0 → −3x + 4y = 0
4

sposób Janka191 znacznie krótszy !