Odbicie wykresu funkcji względem prostej the foxi: Podaj wzór funkcji, której wykres otrzymano w wyniku przekształcenia paraboli o równaniu y=x²+4x−5 przez symetrię względem prostej y=−5 Czy mógłby mnie ktoś troszeczkę naprowadzić na rozwiązanie? Miałem zamiar narysować wykres, najważniejsze punkty jak miejsca zerowe czy wierzchołek odbić względem y=−5 i z tak otrzymanych punktów wyłuskać wzór nowej funkcji. Jest pewnie jakieś bardziej uniwersalne rozwiązanie, proszę o pomoc.

5-latek: Wykresy funkcji sa symetryczne wzgledem prostej y=k ⇔⋀x∊D f(x)−k= k−g(x) ⇔f(x)+g(x)=2k Sa symetryczne wzgledem prostej o rownaniu x=p ⇔ f(x)= g(p−(x−p))⇔f(x)= g(2p−x)

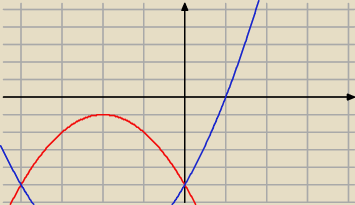
Mac Donald: y+5=−(x²+4x)

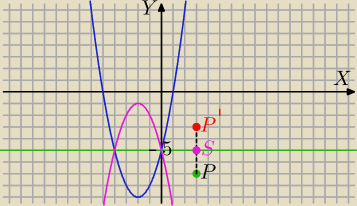
Mila: (*) y=x²+4x−5 P=(x,y) wyprowadzimy wzór na wsp. P' (x',y') symetrycznego do P względem prostej y=−5 S=(x,−5) − środek odcinka PP' x'=x

	y+y'
−5=		⇔y'=−10−y⇔y=−10−y'
	2

podstawiamy do (*) −10−y'=x'²+4x'−5 y'=−x'²−4x−5 y=−x²−4x−5

5-latek: Dobry wieczor Milu

Mila: Dobry wieczór

the foxi: Mila, dziękuję za wytłumaczenie. (: