Liczby zespolone
Paweł: korzystając z interpretacji geometrycznej modułu róznicy liczb zespolonych wyznaczyc i
narysować zbiory liczb zespolonych spelniajacych warunki
|z−1|=|1+5i−z|
23 paź 15:29
Jack:
Korzystam z :
z = a + bi oraz |z| =
√a2+b2
zatem
|a+bi−1| = |1+5i−a−bi|
|a−1 + bi| = |1−a + i(5−b)|
(a−1)
2 + b
2 = (1−a)
2 + (5−b)
2
a
2−2a+1 +b
2 = 1−2a+a
2 + 25−10b+b
2
b
2 = 25−10b+b
2
10b=25
| | 5 | |
Zatem rozwiązaniem jest punkt na |
| na osi Im(z) |
| | 2 | |
23 paź 17:47
Jack: | | 5 | |
Oczywiscie chodzi o prosta Im(z) = |
| |
| | 2 | |
23 paź 17:48
Mila:
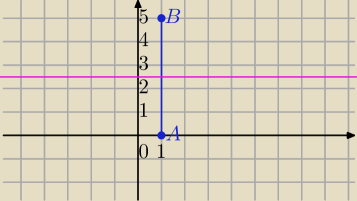
|z−1|=|1+5i−z|⇔
|z−1|=|(−1)*(z−(1+5i)|
|z−(1+0i)|=|z−(1+5i)|
Szukany zbiór punktów to symetralna odcinka o końcach:
A=(1,0) i B=(1,5)
23 paź 18:16
 |z−1|=|1+5i−z|⇔
|z−1|=|(−1)*(z−(1+5i)|
|z−(1+0i)|=|z−(1+5i)|
Szukany zbiór punktów to symetralna odcinka o końcach:
A=(1,0) i B=(1,5)
|z−1|=|1+5i−z|⇔
|z−1|=|(−1)*(z−(1+5i)|
|z−(1+0i)|=|z−(1+5i)|
Szukany zbiór punktów to symetralna odcinka o końcach:
A=(1,0) i B=(1,5)