Nierówność z wartoscią bezwzględną
Krzysztof Bądaruk: |x+1/x|>1 Witam wszystkich, rozwiązał by ktoś taką nierówność z wartością bezwzględną?
22 paź 15:58
the foxi: | | x+1 | |
|x+1x|>1 czy | |
| |>1 ? |
| | x | |
22 paź 16:01
Krzysztof Bądaruk: x+1 licznik
x mianownik
Pierwszy mój post tutaj i nie bardzo się orientuję jeszcze

22 paź 16:14
the foxi: x≠0
Pierwszy przypadek:
x
2+x>x
2
x>0
Drugi przypadek:
x
2+x<−x
2
2x
2+x<0
2x(x+
12)<0
x∊(−12;0)
W tym przypadku bierzemy sumę przedziałów, czyli
x∊(−12;0)∪{0;+∞)
22 paź 16:21
Krzysztof Bądaruk: Takie pytanko, w tym drugim przypadku nie powinno być takiego przedziału x∊(−∞;−1/2) gdy tam
jest x<−1/2
22 paź 16:38
the foxi: Nieee, po lewej stronie mamy postać iloczynową funkcji kwadratowej. Jej miejsca zerowe to 0 i
−12, a ramiona paraboli są skierowane ku górze.
Nas interesują iksy, dla których parabola leży poniżej osi OX, więc są to liczby z przedziału
(−12;0).
22 paź 16:59
jc: Niektórzy na forum wiedzą, że uczniowie nie pamiętają o nawiasach i poprawiają tekst zadań.
Potem uczniowie dostają dwóje za brak nawiasów.
|(x+1)/x| > 1
|x+1| > |x|
punkty oddalone bardziej od −1 niż od 0, czyli x > −1/2,
ale bez x=0 bo nie wolno dzielić przez zero.
22 paź 17:06
Krzysztof Bądaruk: Bardzo dziękuję the foxi za wyjaśnienie i jc za słuszna uwagę

22 paź 17:14
jc: Rozwiąż taką nierówność: |(x−3)/(x−7)| > 1.
22 paź 17:25
Krzysztof Bądaruk: Pierwszy przypadek:
(x−3)/(X−7)>1 /*(x−7)
(x−3)(x−7)>(x−7)
X2−7x−3x+21>x−7
X2−10x +21>x−7
X2−11x+28>0
Delta=9
X1=4
X2=7
x∊(4;7)
Dobry tok rozumowania? Liczyć drugi przypadek w ten sposób?
22 paź 18:20
jc:
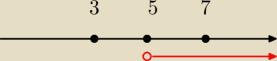
|(x−3)/(x−7)| > 1
|x−3| > |x−7|
Nierówność |x−3| > |x−7| oznacza, że odległość x od 3 jest większa niż odległość
x od 7. Tak jest dla x > 5 (liczba 5 leży w połowie drogi od 3 do 7).
Z oczywistych powodów 7 odrzucamy.
Piszę, abyś zobaczył, że w tym zadaniu nie trzeba nic liczyć, ani rozważać przypadków.
22 paź 18:37


 |(x−3)/(x−7)| > 1
|x−3| > |x−7|
Nierówność |x−3| > |x−7| oznacza, że odległość x od 3 jest większa niż odległość
x od 7. Tak jest dla x > 5 (liczba 5 leży w połowie drogi od 3 do 7).
Z oczywistych powodów 7 odrzucamy.
Piszę, abyś zobaczył, że w tym zadaniu nie trzeba nic liczyć, ani rozważać przypadków.
|(x−3)/(x−7)| > 1
|x−3| > |x−7|
Nierówność |x−3| > |x−7| oznacza, że odległość x od 3 jest większa niż odległość
x od 7. Tak jest dla x > 5 (liczba 5 leży w połowie drogi od 3 do 7).
Z oczywistych powodów 7 odrzucamy.
Piszę, abyś zobaczył, że w tym zadaniu nie trzeba nic liczyć, ani rozważać przypadków.