the foxi: Oblicz ekstrema tej funkcji.
f(x)=81x
4−9x
2+6x+7 −> f'(x)=324x
3−18x+6
Z twierdzenia o pierwiastkach wymiernych f'(−
13)=0 i to jest jedyny pierwiastek
rzeczywisty.
Współczynnik przy a
3>0, więc funkcja f maleje do −u(1)(3), potem rośnie − zatem ma w tym
punkcie minimum.
f(−
13)=5.
W −
∞ i +
∞ funkcja przyjmuje wartości +
∞, zatem liczba 5 jest jej najmniejszą wartością.
Czyli nierówność jest spełniona dla każdej liczby.
the foxi: Haha, okazuje się, że są szybsze metody, a ja zawsze wybieram tę okrężną.
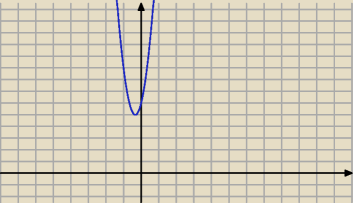81x4−9x2+6x+7>0
81x4−9x2+6x+7=81x4−18x2+1+9x2+6x+6=
(9x2−1)2+(9x2+6x+6)>0
(9x2−1)2≥0
9x2+6x+6>0 , Δ<0 i a>0