Nierówność geo Krzysztof99: Wykaż że jeśli a,b,c,d to długości kolejnych boków czworokąta wypukłego, a S to jego pole, to ab+bc+cd+da≥4S.

Krzysztof99: Inaczej (tak było w treści): wykaż, że ((a+c)/2)*((b+d)/2)≥S . Jestem na telefonie, to mnożenie ułamków o mianownikach 2, a liczniki to a+c i b+d, a zależy mi na szybkim rozwiązaniu albo wskazówce, bo nic nie mogę wymyślić.

PW: Czy to prawda, że pole trójkąta jest mniejsze niż połowa iloczynu długości dwóch jego boków (w szczególnym przypadku równe)?

Eta: Nie napiszę rozwiązania..... bo PW znowu będzie na mnie krzyczał : "zepsuła, zepsuła"

PW: Słusznie, niech adept najpierw sam pomyśli,

Eta:

Krzysztof99: Tak no to z sinusów wychodzi, ale rozważałem to i to nic mi nie daje, bo to nie wyjdzie pole czworokąta według mnie, ale trójkąt ucięcty przez przekątną i to mi nie da pola czworokąta, chyba że gdzieś tu mam błąd, to proszę pomóc

PW: Eta ma rozwiązanie.

Krzysztof99: To prosiłbym jak najszybciej albo jakąś dużą wskazówkę, bo to pilne, tj. na jutro.

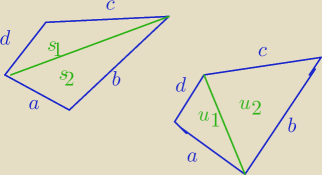
Mila: s₁+s₂=S u₁+u₂=S

1
	a*b≥s2
2

1
	c*d≥s1
2

1		1
	a*b+		c*d≥S
2		2

a*b+c*d≥2S Dalej sam z drugim trójkątem

Mila: Z drugim podziałem czworokąta.

Eta: 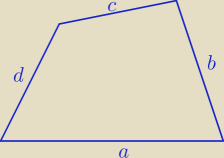2 sposób Jeżeli w taki czworokąt o kolejnych bokach a,b,c,d da się wpisać okrąg i da się na nim opisać okrąg to pole S=√abcd [j²] Można ten wzór łatwo wyprowadzić Z nierówności między średnimi arytmetyczną i geometryczną mamy:

a+c		b+d
	≥√ac i		≥√bd
2		2

mnożąc stronami

a+c		b+d
	*		≥√abcd=S
2		2

Krzysztof99: Dziękuję bardzo wszystkim