Liczby zespolone, zbiór funkcji
Łukasz: Narysuj zbiór funkcji:
| z−(4+3i) | < 2
Re z = Im z
3 Re z+1z−1 =0
Pierwsze dwa w klamerce.
Z góry dziękuję.
19 paź 18:29
Mila:
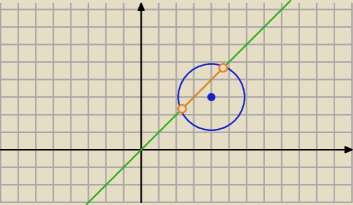
Nie ma tu funkcji, możesz znaleźć zbiór punktów spełniających te warunki.
|z−(4+3i)| <2 wnętrze koła o środku (4,3) i r=2
i
Re (z)=im(z)
z=x+iy , x,y∊R
x=y prosta
część wspólna
19 paź 20:29
Mila:
2)
z≠1+0i
z=x+iy , x,y∊R
| | z+1 | | x+iy+1 | | (x+1)+iy | | (x−1)−iy | |
u= |
| = |
| = |
| * |
| = |
| | z−1 | | x+iy−1 | | (x−1)+iy | | (x−1)−iy | |
| | (x2+y2−1)−2y i | |
= |
| |
| | (x−1)2+y2 | |
| | (x2+y2−1) | |
Re(u)= |
| =0 |
| | (x−1)2+y2 | |
x
2+y
2=1 okrąg bez punktu (1,0)
19 paź 20:42
Łukasz: Co do pierwszego:
Znalazłem takie rozwiązanie:
|z|−|4+3i|<2
|z|−√16+9<2
|z|−5<2
|z|<7
I wtedy wychodzi inaczej, ale nie wiem czy po drodze nie ma jakiegoś błędu.
19 paź 22:51
Mila:
|z−(4+3i)|<2
z=x+iy, x,y∊R
|x+iy−4−3i|<2⇔
|(x−4)+i*(y−3)|<2
√(x−4)2+(y−3)2<2 /2
(x−4)2+(y−3)2<22 i masz
równanie okręgu (x−4)2+(y−3)2=4
a ponieważ masz nierówność to szukany obszar to wnętrze , tak jak napisałam.
19 paź 22:57