pole czworokata gość: Przekątne równoległoboku o polu równym 16√2 cm² przecinają się pod kątem, którego sinus

	2 √2
wynosi		. Jedna z przekątnych tego równoległoboku jest trzykrotnie dłuższa od
	2

drugiej. a) Uzasadnij, że krótsze boki tego równoległoboku są prostopadłe do jednej z przekątnych b) oblicz obwód tego równoległoboku Proszę o wyjaśnienie tego zadania, obliczyłem najpierw przekątne, ale nie wiem co dalej

Mila: sinus nie może mieć takiej wartości. |sinx|≤1

gość: fakt, źle przepisałem. jest podzielić przez 3

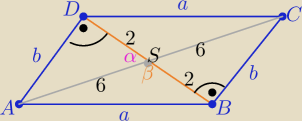
Eta: |BC|=e

	1
|AC|=f=3e P=		e*f *sinα ⇒ ............ e=4 to f=12
	2

	1
cosα= √1−sin2α =..=
	3

z tw. cosinusów w ΔASD i w Δ ASB b²=40−8 ⇒ b=4√2 a²=40+8 ⇒ a=4√3 Trójkąty ABD i DBC są prostokątne bo b²+e²=a² ( 32+16=48 Obwód : 2a+2b=...............

Mila:

	2√2
sinα=
	3

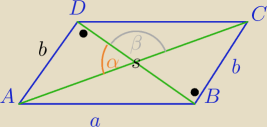
P=16√2 |AC|=3*|BD|

	1
1) PΔASD=		*16√2=4√2
	4

	1		1		1
PΔASD=		*(		|BD|*		|AC|*sinα
	2		2		2

1		2√2
	*|BD|**3|BD|*		=4√2
8		3

|BD|=4| |AC|=12 2) sin²α+cos²α=1

	2√2		1
cos2α=1−(		)2=
	3		9

	1		1
cosα=		, cosβ=−
	3		3

3) W ΔASD: |DS|=2, |AS|=6

	1
b2=22+62−2*2*6*
	3

b²=32 b=4√2 4) W ΔDSC:

	1
a2=22+62+2*2*6*
	3

a²=48 a=4√3 5) W ΔASD: 6²= ? 2²+b² L=36 P=4+(4√2)²=4+32=36 ⇔ΔADS jest prostokątny. b) ob=2a+2b licz posprawdzaj rachunki.

Eta: Posprawdzałam Dla Mili

Mila: Dziękuję

gość: a czy jest inny sposób? jeśli jeszcze nie było twierdzenia cosinusów

Mila: W której jesteś klasie, na jakim poziomie ma być rozwiązanie?

gość: 1 liceum, poziom rozszerzony. to temat z planimetrii − pole czworokąta

Mila: Popatrz tu po 20.

gość: ok, dziękuje bardzo

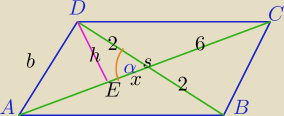
Mila: 1) korzystamy z obliczonych długości przekątnych. 2) W ΔDES:

	h		2√2		h
sinα=		⇔		=
	|DS|		3		2

	4√2
h=
	3

h²+x²=|DS|²

	4√2
(		)2+x2=4
	3

	32		4
x2=4−		=
	9		9

	2
x=
	3

	2		16
3) |AE|=6−		=
	3		3

W ΔAED: b²=h²+|AE|²

	4√2		16
b2=(		)2+(		)2
	3		3

	32		256
b2=		+
	9		9

	288		144*2
b2=		=		⇔
	9		9

	12√2
b=
	3

[N[b=4√2 4) W ΔDEC:

	2		20
|EC|=6+x=6+		=
	3		3

a²=h²+|EC|²

	32		400		432		16*9*3
a2=		+		=		=
	9		9		9		9

	4*3√3
a=
	3

a=4√3 =================== Dalej chyba wiadomo.

gość: Żeby uzasadnić, że krótsze boki są prostopadłe do przekątnej wystarczy podstawić do tw. Pitagorasa? to kończy dowód?

Mila: Tak, masz przecież wyżej zrobione. 22:17

gość: dziękuję za pomoc

Mila: