figury podobne klaudiaa: Dany jest równoległobok R₁, którego boki maja długość 4 cm i 6 cm. Jedna z przekątnych tego równoległoboku jest prostopadła do jego krótszych boków. Równoległobok R₂ o polu 200√5 cm² jest podobny do równoległoboku R₁. Oblicz obwód równoległoboku R₂

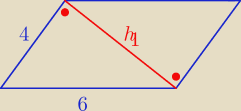
Janek191: Mamy 4² + h₁² = 6² h₁² = 36 − 16 = 20 = 4*5 h₁ = 2√5 więc P₁ = 4 h₁ = 4* 2√5 = 8 √5 oraz P₂ = 200 √5 zatem

p2		200 √5
	=		= 25 = k2 ⇒ k = 5 − skala podobieństwa
p1		8 √5

L₁ = 2*6 + 2* 4 = 20 zatem L₂ = k*L₁ = 5*20 = 100 ========================

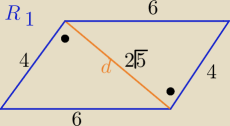
Eta: R₁: d=√36−16=√20=2√5 P(R₁)=4*2√5=8√5 P(R₂)=200√5

P(R2)		200√5
	=k2 ⇒ k2=		=25 ⇒ k=5
P(R1)		8√5

Obwód R₂=k*Obwód R₁= 5*(8+12)=.........