Liczby zespolone
Klimno: Oblicz pierwiastki wykorzystując postać trygonometryczną liczby zespolonej.
Wyniki podaj w postaci algebraicznej.
4√−4
Mi wyszło: √2, i*√2, −√2, −i*√2
A odpowiedzi to podobno:
1+i, 1−i, −1−i, −1+i.
17 paź 16:17
kochanus_niepospolitus:
4√−4 = 4√(2i)2 = √2i
17 paź 16:23
kochanus_niepospolitus:
i oczywiście −√2i
17 paź 16:23
Klimno: Ten minus został wyłączony przed pierwiastek? Czy skąd się wziął?
17 paź 16:41
Klimno: czy koś mógłby rozpisać te postacie trygonometryczne

17 paź 17:07
Adamm: x4=−4
x4+4=0
x4−(2i)2=0
(x2−2i)(x2+2i)=0
2i=(1+i)2
−2i=(1−i)2
(x2−(1+i)2)(x2−(1−i)2)=0
(x−(1+i))(x+(1+i))(x−(1−i))(x+(1−i))=0
x=1+i lub x=−1−i lub x=1−i lub x=−1+i
17 paź 17:21
Klimno: mógłby ktoś obliczyć to postacią trygonometryczną , ponieważ tak brzmiało zadnie?
17 paź 17:26
Klimno: bardzo proszę o pomoc
17 paź 18:04
Klimno: Czy nikt nie umie tego zrobić?
17 paź 19:13
jc: Stosujesz wzór:
z = 41/4(cos π/4 + i sin π/4) (cos 2kπ/4 + i sin 2kπ/4), k=0,1,2,3
Choć to bez sensu, bo wynik jest oczywisty.
17 paź 19:30
Klimno: wynik wychodzi zły z tego wzoru
17 paź 19:35
Klimno: Mi cągle wychodzą tylko dwa wyniki

17 paź 20:41
Mila:
No to wg wzoru ;
z=−4
|z|=4
φ=π
| | π+2kπ | | π+2kπ | |
zk=4√4*( cos |
| +i sin |
| ) gdzie k∊{0,1,2,3} |
| | 4 | | 4 | |
4√4=
√2
| | π | | π | | √2 | | √2 | |
z0=√2*(cos |
| +isin |
| )=√2*( |
| +i * |
| )=1+i |
| | 4 | | 4 | | 2 | | 2 | |
| | 3π | | 3π | | √2 | | √2 | |
z1=√2*(cos |
| +isin |
| )=√2*(− |
| +i * |
| )=−1+i |
| | 4 | | 4 | | 2 | | 2 | |
| | 5π | | 5π | | √2 | | √2 | |
z2=√2*(cos |
| +isin |
| )=√2*(− |
| −i * |
| )=−1−i |
| | 4 | | 4 | | 2 | | 2 | |
| | 7π | | 7π | | √2 | | √2 | |
z3=√2*(cos |
| +isin |
| )=√2*( |
| −i * |
| )=1−i |
| | 4 | | 4 | | 2 | | 2 | |
17 paź 21:17
Romeo: z talii 24 kart wybrano jednego pika , jednego kiera i jedno karo . wiadomo że nie wybrano ani
trzech króli , ani trzech dam . ile jest możliwości takiego wyboru ?
17 paź 21:23
Romeo: Z talii 24 kart wybrano sześć , wśród których były cztery asy . pozostałe dwie karty to albo
król i dama , albo dama i walet. ile jest możliwości takiego wyboru ?
Proszę o pomoc ( na jutro rano muszę mieć) dziękuję
17 paź 21:27
Klimno: Mila dlaczego kont jest równy pi?
17 paź 21:31
Klimno: kąt*
17 paź 21:31
Klimno: Skoro π to druga ćwiartka nie powinniśmy zredukować do pierwszej

17 paź 21:40
PW: −4=4(cosπ+isinπ) − taka jest postać trygonometryczna liczby −4.
Szukając jej pierwiastka czwartego stopnia obliczamy
4√4 (pierwiastek czwartego stopnia z
modułu, a kąt dzielimy przez 4:
| | π | | π | | √2 | | √2 | |
z0 = 4√4(cos |
| +isin |
| ) = √2( |
| +i |
| )=1+i. |
| | 4 | | 4 | | 2 | | 2 | |
Inne pierwiastki podane we wzorze na a
k ...
17 paź 22:04
Klimno: Dlaczego nie redukujemy π do pierwszej ćwiartki?
17 paź 22:09
Mila:
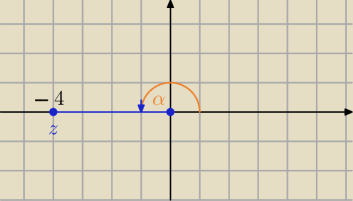
z=−4
17 paź 22:09
Klimno: ale dlaczego nie redukujemy tego kąta do pierwszej ćwiartki

17 paź 22:11
17 paź 22:11
Mila:
poczytaj :
Argument główny liczby zespolonej
17 paź 22:13
Klimno: Czyli gdy kąt π3 będzie w IV ćwiartce to muszę zredukować?
17 paź 22:23
Klimno: kiedy mogę używać tego że: w II ćwiartce π−φ w III π+φ a w IV 2π−φ

17 paź 22:28
Mila:
Nie wiem o co Ci chodzi?
| | 3π | |
Czy o obliczenie cos |
| ? |
| | 4 | |
17 paź 22:58
Klimno: chodzi mi oto że czasmi np. jak jest cosφ=12 a sinφ= −√32 jest to π3 i kąt
należy do IV ćwiartki wię należy zrobić 2π−π3
więc dlaczego nie stosujemy tego do w/w zadania?
17 paź 23:05
Mila:
Masz po pierwiastkiem liczbę:
z=−4+0i
|z|=4
Jest tylko jeden kąt w przedziale <0,2π>, który spełnia ten warunek.
φ=π
I co tu chcesz redukować?
Poczytaj co to jest argument liczby zespolonej.
Masz narysowany 22:09.
17 paź 23:44
Mila:
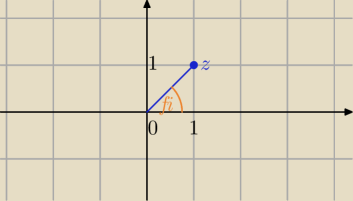
z=1+1i
Możesz liczyć i wyjdzie to samo.
17 paź 23:47



 z=−4
z=−4


 z=1+1i
z=1+1i