Liczby zespolone Michał: Podaj interpretację geometryczną liczb zespolonych: a) 2 ≤ |iz − 5| < 3

	|z + 1|
b)		≥ 1
	|z2 + 1|

c) sin (π |z + 2i|) > 0

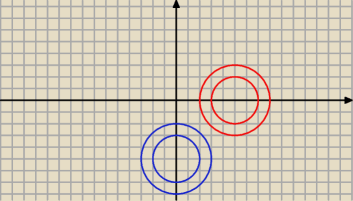
Adam: u=iż z=−iu −i=cos(3π/2)+isin(3π/2) <− obrót o 3π/2 przeciwnie do ruchu zegara 2≤|u−5|≤3 <− czerwony pierścień (obszar między okręgiem o promieniu 2, a promieniem o promieniu 3, oba o środkach (5; 0)) 2≤|iz−5|≤3 <− niebieski pierścień (po obrocie)

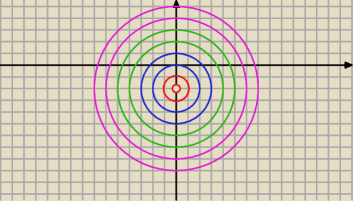
Adam: sin(pi|z+2i|)>0 ⇔ 2k<|z+2i|<2k+1 dla k=0, 1, ... jest to zbiór takich pierścieni, wszystkie o środku (0; −2)

Jerzy: W b) nie masz przypadkiem " i " , zamiast 1 pod modułami ?

Michał: Racja. W b) ma być z + i na górze, z² + 1 w mianowniku.

Adamm: no to łatwe z²+1=(z−i)(z+i) skróć ze sobą mianownik z licznikiem, wiedząc że |z|*|w|=|zw| (pamiętaj o dziedzinie)

Michał: Na czym dokładnie polega metoda u = iz ; z = −iu, którą zastosowałeś do podpunktu a)?

PW: Skoro u = iz, o po pomnożeniu stronami przez i iu = i²z iu = −z z = −iu